
【題目】(探究)如圖①,在四邊形ABCD中,∠A=∠C=90°,AD=CD,點E、F分別在邊AB、BC上,ED=FD,證明:∠ADE=∠CDF.
(拓展)如圖②,在菱形ABCD中,∠A=120°,點E、F分別在邊AB、BC上,ED=FD.若∠EDF=30°,求∠CDF的大小.

【答案】【探究】證明解析;【拓展】∠CDF=15°.
【解析】
(探究)根據HL證明Rt△AED≌Rt△CFD,可得結論;
(拓展)如圖②,作輔助線,構建全等三角形,證明△AMD≌△CND,則MD=CN,∠MDA=∠NDC,根據菱形的性質得:∠ADC=60°,所以∠CDF+∠ADE=60°-30°=30°,可得結論.
(探究)如圖①,在Rt△AED和Rt△CFD中,
∵![]() ,
,
∴Rt△AED≌Rt△CFD(HL),
∴∠ADE=∠CDF;
(拓展)解:如圖②,過點D作DM⊥BA交BA延長線于點M,作DN⊥BC交BC延長線于點N,
∴∠AMD=∠CND=90°,
∵四邊形ABCD是菱形,
∴AD=CD,∠BAD=∠BCD,
∴∠MAD=∠NCD,
∴△AMD≌△CND,
∴MD=CN,∠MDA=∠NDC,
由探究得:∠MDE=∠NDF,
∴∠MDE﹣∠MDA=∠NDF﹣∠NDC,即∠ADE=∠CDF,
∵四邊形ABCD是菱形,∠BAC=120°,
∴∠ADC=60°,
∵∠EDF=30°,
∴∠CDF+∠ADE=60°﹣30°=30°,
∵∠ADE=∠CDF,
∴∠CDF=15°.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】如圖,某農場老板準備建造一個矩形羊圈![]() ,他打算讓矩形羊圈的一面完全靠著墻
,他打算讓矩形羊圈的一面完全靠著墻![]() ,墻
,墻![]() 可利用的長度為
可利用的長度為![]() ,另外三面用長度為
,另外三面用長度為![]() 的籬笆圍成(籬笆正好要全部用完,且不考慮接頭的部分),設矩形羊圈的面積為
的籬笆圍成(籬笆正好要全部用完,且不考慮接頭的部分),設矩形羊圈的面積為![]() ,垂直于墻的一邊長
,垂直于墻的一邊長![]() 為
為![]() .
.

![]() 填空:
填空:![]() 與
與![]() 的函數關系式________,
的函數關系式________,![]() 是
是![]() 的________函數,
的________函數,![]() 的取值范圍是________;
的取值范圍是________;
![]() 若要使矩形羊圈的面積為
若要使矩形羊圈的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平面直角坐標系中,△ABC的三個頂點的坐標分別為A(2,2),B(1,﹣1),C(3,0).

(1)在圖1中,畫出以點O為位似中心,放大△ABC到原來的2倍的△A1B1C1;
(2)若P(a,b)是AB邊上一點,平移△ABC之后,點P的對應點P'的坐標是(a+3,b﹣2),在圖2中畫出平移后的△A2B2C2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小敏的爸爸買了某項體育比賽的一張門票,她和哥哥兩人都想去觀看,可門票只有一張,讀九年級哥哥想了一個辦法,拿出![]() 張撲克牌,將數字
張撲克牌,將數字![]() 、
、![]() 、
、![]() 、
、![]() 的四張給了小敏,將數字
的四張給了小敏,將數字![]() 、
、![]() 、
、![]() 、
、![]() 的四張撲克牌留給自己,并按如下游戲規則進行:小敏和哥哥從各自的四張牌中隨機抽出一張,然后將抽出兩張牌數字相加,如果和為偶數,則小敏去;如果和為奇數,則哥哥去.
的四張撲克牌留給自己,并按如下游戲規則進行:小敏和哥哥從各自的四張牌中隨機抽出一張,然后將抽出兩張牌數字相加,如果和為偶數,則小敏去;如果和為奇數,則哥哥去.
(1)請用畫樹形圖或列表的方法求小敏去看比賽的概率;
(2)小敏知道哥哥設計的游戲規則不公平,于是她提議兩人交換一張牌,使游戲規則公平后再進行比賽,你知道小敏是如何提議的嗎?說說你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校有兩個校區:南校和北校,這兩個校區九年級學生各有300名,為了解這兩個校區九年級學生的英語單詞掌握情況,進行了抽樣調查,過程如下:
①收集數據,從南校和北校兩個校區的九年級各隨機抽取10名學生,進行英語單詞測試,測試成績(百分制)如下:
南校 92 100 86 89 73 98 54 95 98 85
北校 100 100 94 83 74 86 75 100 73 75
②整理、描述數據,按如下分數段整理、描述這兩組樣本數據:
成績x 人數 部門 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
南校 | 1 | 0 | 1 | 3 | 5 |
北校 | 0 | 0 | 4 | 2 | 4 |
(說明:成績90分及以上為優秀,80~89分分為良好,60~79分為合格,60分以下為不合格)
③分析數據,對上述數據進行分析,分別求出了兩組樣本數據的平均數、中位數、眾數、方差如下表:
校區 | 平均數 | 中位數 | 眾數 | 方差 |
南校 | 87 | 90.5 |
| 179.4 |
北校 | 86 |
|
| 121.6 |
④得出結論.
結合上述統計全過程,回答下列問題:
(1)補全③中的表格.
(2)請估計北校九年級學生英語單詞掌握優秀的人數.
(3)你認為哪個校區的九年級學生英語單詞掌握得比較好?說明你的理由.(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線MN交AC于點D,交AB于點E.
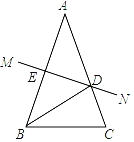
(1)若∠A=40°,求∠DBC的度數;
(2)若AE=6,△CBD的周長為20,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】依據國家實行的《國家學生體質健康標準》,對懷柔區初一學生身高進行抽樣調查,以便總結懷柔區初一學生現存的身高問題,分析其影響因素,為學生的健康發展及學校體育教育改革提出合理項建議.已知懷柔區初一學生有男生840人,女生800人,他們的身高在150≤x<175范圍內,隨機抽取初一學生進行抽樣調查.抽取的樣本中,男生比女生多2人,利用所得數據繪制如下統計圖表:

身高情況分組表
組別 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根據統計圖表提供的信息,下列說法中
①抽取男生的樣本中,身高在155≤x<165之間的學生有18人;
②初一學生中女生的身高的中位數在B組;
③抽取的樣本中,抽取女生的樣本容量是38;
④初一學生身高在160≤x<170之間的學生約有800人.
其中合理的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣為了落實中央的“強基惠民工程”,計劃將某村的居民自來水管道進行改造.該工程若由甲隊單獨施工恰好在規定時間內完成;若乙隊單獨施工,則完成工程所需天數是規定天數的1.5倍.如果由甲、乙隊先合做15天,那么余下的工程由甲隊單獨完成還需5天.
(1)這項工程的規定時間是多少天?
(2)已知甲隊每天的施工費用為6500元,乙隊每天的施工費用為3500元.為了縮短工期以減少對居民用水的影響,工程指揮部最終決定該工程由甲、乙隊合做來完成.則該工程施工費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com