【題目】已知一拋物線與x軸的交點是A（﹣2，0），B（1，0），且經過點C（2，8）．
（1）求該拋物線的解析式．
（2）求該拋物線的頂點坐標．
（3）直接寫出當y＞8時，x的取值范圍．
【答案】（1）y=2x2+2x﹣4；（2）（﹣
，﹣
）；（3）當y＞8時，x的取值范圍是x＜﹣3或x＞2
【解析】試題分析：（1）設交點式y=a（x+2）（x-1），然后把C點坐標代入求出a的值即可得到拋物線解析式；
（2）把（1）中的解析式配成頂點式即可得到拋物線頂點坐標；
（3）先求出點C（2，8）關于對稱軸x=-
的對稱點為（-3，8），再根據二次函數的性質即可求解．
試題解析：
（1）折拋物線解析式為y=a（x+2）（x﹣1），
把C（2，8）代入得a41=8，解得a=2，
所以拋物線解析式為y=2（x+2）（x﹣1），
即y=2x2+2x﹣4；
（2）y=2x2+2x﹣4=2（x+
）2﹣
，
所以拋物線的頂點坐標為（﹣
，﹣
）；
（3）∵y=2x2+2x﹣4=2（x+
）2﹣
，
∴對稱軸是直線x=﹣
a=2＞0開口向上，
∴點C（2，8）關于對稱軸的對稱點為（﹣3，8），
∴當y＞8時，x的取值范圍是x＜﹣3或x＞2．
閱讀快車系列答案科目：初中數學 來源： 題型：
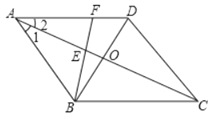
【題目】如圖，已知□ABCD的對角線AC、BD交于O，且∠1=∠2．
（1）求證：□ABCD是菱形；
（2）F為AD上一點,連結BF交AC于E,且AE=AF.求證：AO=
（AF+AB）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在長方形ABCD中，放入6個形狀和大小都相同的小長方形，已知小長方形的長為a，寬為b，且a＞b．
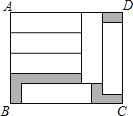
(1)用含a、b的代數式表示長方形ABCD的長AD、寬AB；
(2)用含a、b的代數式表示陰影部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
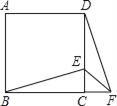
【題目】如圖，正方形ABCD中，E為CD上一點，F為BC延長線上一點，CE=CF．
（1）△DCF可以看作是△BCE繞點C旋轉某個角度得到的嗎？
（2）若∠CEB=60°，求∠EFD的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
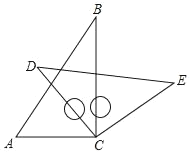
【題目】將一副三角板中的兩塊直角板中的兩個直角頂點重合在一起，即按如圖所示的方式疊放在一起，其中∠A＝60°，∠B＝30，∠D＝45°．
（1）若∠BCD＝45°，求∠ACE的度數．
（2）若∠ACE＝150°，求∠BCD的度數．
（3）由（1）、（2）猜想∠ACE與∠BCD存在什么樣的數量關系并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
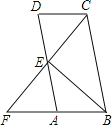
【題目】如圖，已知平行四邊形ABCD中，E為AD中點，CE延長線交BA延長線于點F．
（1）求證：CD=AF；
（2）若BC=2CD，求證：∠F=∠BCF
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y＝kx+b與反比例函數y＝
（x＜0）的圖象相交于點A、點B，與X軸交于點C，其中點A（﹣1，3）和點B（﹣3，n）．
（1）填空：m＝ ，n＝ ．
（2）求一次函數的解析式和△AOB的面積．
（3）根據圖象回答：當x為何值時，kx+b≥（請直接寫出答案） ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在等邊三角形ABC中，BC＝8cm，射線AG∥BC，點E從點A出發沿射線AG以1cm/s的速度運動，同時點F從點B出發沿射線BC以2cm/s的速度運動，設運動時間為t（s）．
（1）連接EF，當EF經過AC邊的中點D時，求證：四邊形AFCE是平行四邊形；
（2）填空：①當t為 s時，四邊形ACFE是菱形；②當t為 s時，△ACE的面積是△ACF的面積的2倍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角墻角AOB（OA⊥OB，且OA、OB長度不限）中，要砌20m長的墻，與直角墻角AOB圍成地面為矩形的儲倉，且地面矩形AOBC的面積為96m2．
（1）求地面矩形AOBC的長；
（2）有規格為0.80×0.80和1.00×1.00（單位：m）的地板磚單價分別為55元/塊和80元/塊，若只選其中一種地板磚都恰好能鋪滿儲倉的矩形地面（不計縫隙），用哪一種規格的地板磚費用較少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com