
【題目】已知二次函數![]() (
(![]() )的圖象如圖所示,對稱軸為
)的圖象如圖所示,對稱軸為![]() .有下列4個結論:①
.有下列4個結論:①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時,![]() 隨
隨![]() 的增大而增大.其中,正確的結論有( )
的增大而增大.其中,正確的結論有( )

A.1個B.2個C.3個D.4個
【答案】C
【解析】
由二次函數的性質和二次函數對稱軸,確定a,b,c的符號,即可判定①;由圖像可知當x=-1時,函數值小于0,即可以將x=-1代入函數解析式,化簡即可判斷②,又由對稱軸為x=-![]() ,即可求得a=b>0,將x=1代入函數解析式,得出a、b、c的關系,將a把b換下來,求出b與c的關系,再進行變形判斷即可解決③,根據二次函數的性質,結合圖像即可判斷④.
,即可求得a=b>0,將x=1代入函數解析式,得出a、b、c的關系,將a把b換下來,求出b與c的關系,再進行變形判斷即可解決③,根據二次函數的性質,結合圖像即可判斷④.
解:由二次函數圖像和性質可知,a>0,c<0,
∵![]()
∴a=b>0,
∴![]() ,
,
故①正確;
由圖像可知當x=-1時,函數值小于0,
即a-b+c<0,
b>a+c,
故②錯誤;
由圖像可知當x=1時,函數值<0,
即a+b+c<0,
∵a=b,
∴2b+c<0,
即2b<-c,
∴8b<-4c,
∵b>0,
∴3b<8b,
∴3b<-4c.
故③正確;
根據函數圖像可知,函數在對稱軸的右側y隨x的增大而增大,
∵二次函數的對稱軸為x=-![]() ,
,
∴當![]() 時,
時,![]() 隨
隨![]() 的增大而增大.
的增大而增大.
故④正確.
故本題答案為:C.


科目:初中數學 來源: 題型:
【題目】一組正方形按如圖所示放置,其中頂點 B1 在 y 軸上,頂點 C1,E1,E2,C2,E3,E4,C3… 在 x 軸上.已知正方形 A1B1C1D1 的邊長為 1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,則正方形 A2020B2020C2020D2020 的邊長是______.
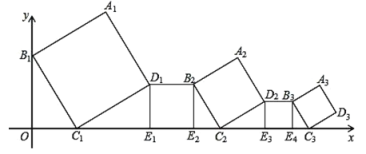
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的網格中,給出了格點△ABC(頂點為網格線的交點).
(1)將△ABC先向下平移3個單位長度,再向右平移4個單位長度后得到△A1B1C1.畫出平移后的圖形;
(2)將△ABC繞點A1順時針旋轉90°后得到△A2B2C2.畫出旋轉后的圖形;
(3)借助網格,利用無刻度直尺畫出△A1B1C1的中線A1D1(畫圖中要體現找關鍵點的方法).
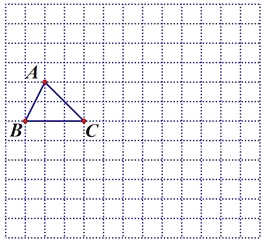
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課程:樂器、舞蹈、繪畫、書法,學校采取隨機抽樣的方法進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門).對調查的結果進行整理,繪制成如下兩幅不完整的統計圖,請結合圖中所給信息解答下列問題:
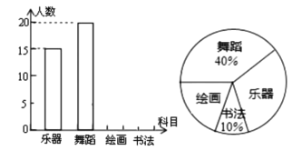
(1)本次共調查了多少名學生?
(2)請將條形統計圖補充完整;
(3)在被調查的學生中,選修書法的有2名男同學,其余為女同學,現要從中隨機抽取2名同學代表學校參加某社區組織的書法活動,請你用列表或畫樹狀圖的方法,求所抽取的2名同學恰好是1名男同學和1名女同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在美化校園的活動中,數學興趣小組用16m長的籬笆,一邊靠墻圍成一個矩形花園ABCD,墻長為6m,設AB![]() m.
m.
(1)若花園的面積為14![]() ,求
,求![]() 的值;
的值;
(2)花園的面積能否為40![]() ?為什么?
?為什么?
(3)若要求花園的面積大于24![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀材料,再解答問題:
已知點![]() 和直線
和直線![]() ,則點
,則點![]() 到直線
到直線![]() 的距離
的距離![]() 可用公式
可用公式![]() 計算.例如:求點
計算.例如:求點![]() 到直線
到直線![]() 的距離.
的距離.
解:由直線![]() 可知:
可知:![]() .
.
所以點![]() 到直線
到直線![]() 的距離為
的距離為![]()
![]() .
.
求:(1)已知直線![]() 與
與![]() 平行,求這兩條平行線之間的距離;
平行,求這兩條平行線之間的距離;
(2)已知直線![]() 分別交
分別交![]() 軸于
軸于![]() 兩點,
兩點,![]() 是以
是以![]() 為圓心,
為圓心,![]() 為半徑的圓,
為半徑的圓,![]() 為
為![]() 上的動點,試求
上的動點,試求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“足球運球”是中考體育必考項目之一.我市某學校為了解今年九年級學生足球運球的掌握情況,隨機抽取部分九年級學生足球運球的測試成績作為一個樣本,按A、B、C、D四個等級進行統計,制成了如圖不完整的統計圖.
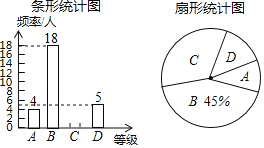
根據所給信息,解答以下問題:
(1)本次抽樣調查抽取了 名學生的成績;在扇形統計圖中,D對應的扇形的圓心角是 度;
(2)補全條形統計圖;
(3)所抽取學生的足球運球測試成績的中位數會落在 等級;
(4)該校九年級有300名學生,請估計足球運球測試成績達到A級的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2022年在北京將舉辦第24屆冬季奧運會,很多學校都開展了冰雪項目學習.如圖,滑雪軌道由AB、BC兩部分組成,AB、BC的長度都為200米,一位同學乘滑雪板沿此軌道由A點滑到了C點,若AB與水平面的夾角α為20°,BC與水平面的夾角β為45°,則他下降的高度為___________米(精確到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com