
【題目】“足球運球”是中考體育必考項目之一.我市某學校為了解今年九年級學生足球運球的掌握情況,隨機抽取部分九年級學生足球運球的測試成績作為一個樣本,按A、B、C、D四個等級進行統計,制成了如圖不完整的統計圖.
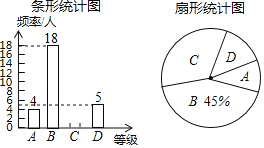
根據所給信息,解答以下問題:
(1)本次抽樣調查抽取了 名學生的成績;在扇形統計圖中,D對應的扇形的圓心角是 度;
(2)補全條形統計圖;
(3)所抽取學生的足球運球測試成績的中位數會落在 等級;
(4)該校九年級有300名學生,請估計足球運球測試成績達到A級的學生有多少人?
【答案】(1)40,45;(2)詳見解析;(3)B;(4)估計足球運球測試成績達到A級的學生有30人
【解析】
(1)根據B等級的人數和B等級所占百分比即可算出總人數,再乘以D等級的占比即可;
(2)根據40﹣4﹣18﹣5=13,畫出即可;
(3)把所有數據從小到大排序,處在第20、21位的兩個數都是B等級,即可得出答案;
(4)用300乘以![]() 即可得到結果;
即可得到結果;
解:(1)18÷45%=40(人),360°×![]() =45°,
=45°,
故答案為:40,45;
(2)40﹣4﹣18﹣5=13,補全條形統計圖如圖所示:
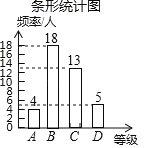
(3)將40名學生的成績從大到小排列后,處在第20、21位的兩個數都是B等級,此中位數是B等級,
故答案為:B;
(4)300×![]() =30(人),
=30(人),
因此,估計足球運球測試成績達到A級的學生有30人.


科目:初中數學 來源: 題型:
【題目】已知二次函數![]() (
(![]() )的圖象如圖所示,對稱軸為
)的圖象如圖所示,對稱軸為![]() .有下列4個結論:①
.有下列4個結論:①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時,![]() 隨
隨![]() 的增大而增大.其中,正確的結論有( )
的增大而增大.其中,正確的結論有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面內容,并解決問題:
《名畫》中的數學
前蘇聯著名科學家別萊利曼在他所著的《趣味代數學》中介紹了波格達諾夫·別列斯基的《名畫》,畫上那位老師拉金斯基是一位自然科學教授,放棄了大學教席(教師職務)來到農村學校當一名普通老師.畫中,黑板上寫著一道式子,如圖所示:

從這道算式計算可以得出答案等于2,如果仔細一研究,10,11,12,13,14這幾個數具有一種有趣的特性:![]() ,而且
,而且![]() .
.
請解答以下問題:
(1)還有沒有其他像這樣五個連續的整數,前三個數的平方和正好等于后兩個數的平方和呢?如果有,請求出另外的五個連續的整數;
(2)若七個連續整數前四個數的平方和等于后三個數的平方和,請直接寫出符合條件的連續整數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是拋物線y1=ax2+bx+c(a≠0)圖象的一部分,拋物線的頂點坐標A(1,3),與x軸的一個交點B(4,0),直線y2=mx+n(m≠0)與拋物線交于A,B兩點,下列結論:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有兩個相等的實數根;④拋物線與x軸的另一個交點是(﹣1,0);⑤當1<x<4時,有y2<y1,
其中正確的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現
如圖1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,連接AC,BD交于點M.填空:
①![]() 的值為 ;
的值為 ;
②∠AMB的度數為 .
(2)類比探究
如圖2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,連接AC交BD的延長線于點M.請判斷![]() 的值及∠AMB的度數,并說明理由;
的值及∠AMB的度數,并說明理由;
(3)拓展延伸
在(2)的條件下,將△OCD繞點O在平面內旋轉,AC,BD所在直線交于點M,若OD=1,OB=![]() ,請直接寫出當點C與點M重合時AC的長.
,請直接寫出當點C與點M重合時AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線a∥b,∠1=40°,∠2=80°,則∠3的度數為( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/15/2485292109684736/2491850430775296/STEM/0502255e02c3498e9234cb6eaef26eb9.png]
A.120°B.130°C.140°D.110°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明準備給長![]() 米,寬
米,寬![]() 米的長方形空地栽種花卉和草坪,圖中I、II、III三個區域分別栽種甲、乙、丙三種花卉,其余區域栽種草坪.四邊形
米的長方形空地栽種花卉和草坪,圖中I、II、III三個區域分別栽種甲、乙、丙三種花卉,其余區域栽種草坪.四邊形![]() 和
和![]() 均為正方形,且各有兩邊與長方形邊重合;矩形
均為正方形,且各有兩邊與長方形邊重合;矩形![]() (區域II)是這兩個正方形的重疊部分,如圖所示.
(區域II)是這兩個正方形的重疊部分,如圖所示.
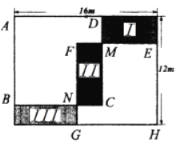
(1)若花卉均價為![]() 元
元![]() ,種植花卉的面積為
,種植花卉的面積為![]()
![]() ,草坪均價為
,草坪均價為![]() 元
元![]() ,且花卉和草坪栽種總價不超過
,且花卉和草坪栽種總價不超過![]() 元,求
元,求![]() 的最大值.
的最大值.
(2)若矩形![]() 滿足
滿足![]() .
.
①求![]() ,
,![]() 的長.
的長.
②若甲、乙、丙三種花卉單價分別為![]() 元
元![]() ,
,![]() 元
元![]() ,
,![]() 元
元![]() ,且邊
,且邊![]() 的長不小于邊
的長不小于邊![]() 長的
長的![]() 倍.求圖中I、II、III三個區域栽種花卉總價
倍.求圖中I、II、III三個區域栽種花卉總價![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
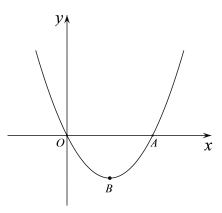
【題目】如圖,拋物線y=x2+mx(m<0)交x軸于O,A兩點,頂點為點B.
(1)求△AOB的面積(用含m的代數式表示);
(2)直線y=kx+b(k>0)過點B,且與拋物線交于另一點D(點D與點A不重合),交y軸于點C.過點C作CE∥AB交x軸于點E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范圍;
<3,求k的取值范圍;
(ⅱ) 求證:DE∥y軸.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com