
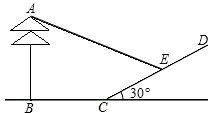
 在同一時刻,1m長的標尺的影長為2m,現測得一棵大樹AB離山坡CD的距離BC=4m,大樹在山坡上的影子長CE=4m,山坡與地平面成30°的角,如圖所示,則大樹的高度為________ m.
在同一時刻,1m長的標尺的影長為2m,現測得一棵大樹AB離山坡CD的距離BC=4m,大樹在山坡上的影子長CE=4m,山坡與地平面成30°的角,如圖所示,則大樹的高度為________ m. )
) CE=2,由勾股定理求出CF=2
CE=2,由勾股定理求出CF=2 ,根據在同一時刻,1m長的標尺的影長為2m求出EF的影子長FQ,求出AB的影子長,即可求出AB.
,根據在同一時刻,1m長的標尺的影長為2m求出EF的影子長FQ,求出AB的影子長,即可求出AB.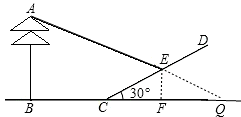 延長AE交BC延長線于Q,過E作EF⊥BC于F,
延長AE交BC延長線于Q,過E作EF⊥BC于F, CE=2,
CE=2, =2
=2 ,
, =
= ,
, +4=8+2
+4=8+2 ,
,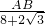 =
= ,
, (m).
(m). ).
).

科目:初中數學 來源: 題型:
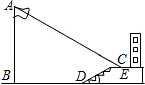 梅華中學九年級數學課外學習小組某下午實踐活動課時,測量朝西教學樓前的旗桿AB的高度.如圖,當陽光從正西方向照射過來時,旗桿AB的頂端A的影子落在教學樓前的坪地C處,測得影長CE=2m,DE=4m,BD=20m,DE與地面的夾角α=30度.在同一時刻,測得一根長為1m的直立竹竿的影長恰為4m.根據這些數據求旗桿AB的高度.(可能用到的數據:
梅華中學九年級數學課外學習小組某下午實踐活動課時,測量朝西教學樓前的旗桿AB的高度.如圖,當陽光從正西方向照射過來時,旗桿AB的頂端A的影子落在教學樓前的坪地C處,測得影長CE=2m,DE=4m,BD=20m,DE與地面的夾角α=30度.在同一時刻,測得一根長為1m的直立竹竿的影長恰為4m.根據這些數據求旗桿AB的高度.(可能用到的數據:| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
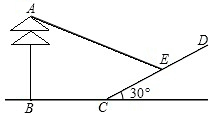 在同一時刻,1m長的標尺的影長為2m,現測得一棵大樹AB離山坡CD的距離BC=4m,大樹在山坡上的影子長CE=4m,山坡與地平面成30°的角,如圖所示,則大樹的高度為
在同一時刻,1m長的標尺的影長為2m,現測得一棵大樹AB離山坡CD的距離BC=4m,大樹在山坡上的影子長CE=4m,山坡與地平面成30°的角,如圖所示,則大樹的高度為| 3 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com