
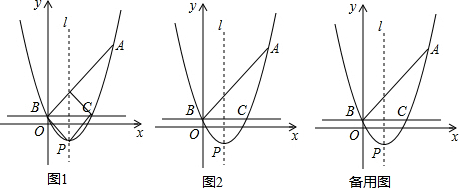
分析 (1)由點A坐標可得拋物線解析式,求出x=0時y的值即可知點B坐標,再根據拋物線對稱性得出點C坐標;
(2)設點P(m,$\frac{1}{3}$m2-2m+1),表示出PD=-$\frac{1}{3}$m2+3m,再用S四邊形PBDC=S△BDC+S△APC=$\frac{1}{2}$BC×PD,建立函數關系式,求出極值即可;
(3)先判斷出PE=CE,再得到∠PCE=∠DBE,以C、P、Q為頂點的三角形與△ABC相似,分兩種情況計算即可.
解答 解:(1)將點A(9,10)代入得:81a-18+1=10,
解得:a=$\frac{1}{3}$,
∴拋物線解析式為y=$\frac{1}{3}$x2-2x+1,
當x=0時,y=1,即點B(0,1),
∵拋物線對稱軸為x=3,
∴點B關于對稱軸的對稱點C坐標為(6,1),
故答案為:y=$\frac{1}{3}$x2-2x+1,(0,1),(6,1);
(2)如圖2,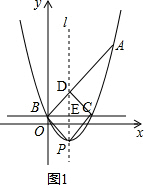
設直線AB的解析式為y=kx+b,
將A(9,10)、B(0,1)代入得:$\left\{\begin{array}{l}{9k+b=10}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直線AB的解析式為y=x+1,
設點P(m,$\frac{1}{3}$m2-2m+1)
∴D(m,m+1)
∴PD=m+1-($\frac{1}{3}$m2-2m+1)=-$\frac{1}{3}$m2+3m,
∵BC⊥PD,BC=6,
∴S四邊形PBDC
=S△BDC+S△APC
=$\frac{1}{2}$BC×DE+$\frac{1}{2}$BC×PE
=$\frac{1}{2}$BC(DE+PE)
=$\frac{1}{2}$BC×PD
=$\frac{1}{2}$×6×(-$\frac{1}{3}$m2+3m)
=-m2+9m
=-(m-$\frac{9}{2}$)2+$\frac{81}{4}$,
∵0<m<6,
∴當m=$\frac{9}{2}$時,四邊形PBDC的面積取得最大值$\frac{81}{4}$,
此時點P的坐標為($\frac{9}{2}$,-$\frac{5}{4}$);
(3)如圖2,
∵y=$\frac{1}{3}$x2-2x+1=$\frac{1}{3}$(x-3)2-2,
∴P(3,-2),
∴PE=yE-yP=3,CE=xE-xC=3,
∴PE=CE,
∴∠PCE=45°
同理可得:∠DBE=45°,
∴∠PCE=∠DBE,
∴在直線AC上存在滿足條件的Q,
設Q(t,1)且AB=9$\sqrt{2}$,BC=6,CP=3$\sqrt{2}$
∵以C、P、Q為頂點的三角形與△ABC相似,
①當△CPQ∽△BAC時,
∴$\frac{CQ}{BC}=\frac{CP}{AB}$,
∴$\frac{6-t}{6}$=$\frac{3\sqrt{2}}{9\sqrt{2}}$,
∴t=4,
∴Q(4,1)
②當△CPQ∽△BCA時,
∴$\frac{CQ}{AB}$=$\frac{CP}{BC}$,
∴$\frac{6-t}{9\sqrt{2}}$=$\frac{3\sqrt{2}}{6}$,
∴t=-3,
∴Q(-3,1),
綜上,點Q的坐標為(4,1)或(-3,1).
點評 此題是二次函數綜合題,主要考查了待定系數法,相似三角形的性質,幾何圖形面積的求法(用割補法),解本題的關鍵是求函數解析式.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:解答題
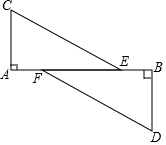 如圖,C、D分別位于路段A、B兩點的正北處與正南處,現有兩車分別從E、F兩處出發,以相同的速度行駛,相同時間后分別到達C、D兩地,休整一段時間后又以原來的速度行駛最終同時到達A、B兩點,那么CE與DF平行嗎?為什么?
如圖,C、D分別位于路段A、B兩點的正北處與正南處,現有兩車分別從E、F兩處出發,以相同的速度行駛,相同時間后分別到達C、D兩地,休整一段時間后又以原來的速度行駛最終同時到達A、B兩點,那么CE與DF平行嗎?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:P是邊長為4厘米的正方形ABCD的邊BC上的點,且PC=1厘米,M是CD邊上的一個動點,
已知:P是邊長為4厘米的正方形ABCD的邊BC上的點,且PC=1厘米,M是CD邊上的一個動點,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com