
【題目】在直角坐標系 xOy 中,拋物線y=ax2+bx+c 上部分點的橫、縱坐標間的對應值如表:

則下列結論正確的是( )
A. 拋物線的開口向下
B. 拋物線的頂點坐標為(2.5,﹣8.75)
C. 當 x>4 時,y 隨 x 的增大而減小
D. 拋物線必經過定點(0,﹣5)
【答案】D
【解析】
根據二次函數的對稱性可知對稱軸為x=2,可知頂點坐標,根據二次函數的增減性可判斷開口方向及x>4時函數的增減性,根據圖像經過(4,-5)及對稱軸是x=2可判斷拋物線必經過定點(0,﹣5).
由表中信息可知:當 x<2 時 y 隨 x 的增大而減小,當 x>2 時,y 隨 x 的增大而減小,
∴拋物線的開口向上,故①錯誤;
由 x=1 時 y=﹣8,x=3 時 y=﹣8 知拋物線的對稱軸為直線x=2,頂點坐標為(2,n),故②錯誤;
∵x>2 時,y 隨 x 的增大而增大,
∴當x>4 時,y 隨 x 的增大而增大,故③錯誤;
∵拋物線的對稱軸為直線 x=2,且拋物線過點(4,﹣5),
∴拋物線必經過定點(0,﹣5),故④正確;
故選:D.


科目:初中數學 來源: 題型:
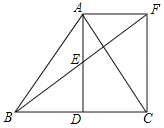
【題目】如圖,△ABC中,D是BC邊上一點,E是AD的中點,過點A作BC的平行線交BE的延長線于F,且AF=CD,連接CF.
(1)求證:△AEF≌△DEB;
(2)若AB=AC,試判斷四邊形ADCF的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
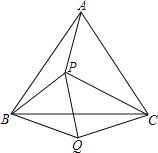
【題目】如圖,P是等邊三角形ABC內的一點,且PA=3,PB=4,PC=5,以BC為邊在△ABC外作△BQC≌△BPA,連接PQ,則以下結論中正確有_____(填序號)①△BPQ是等邊三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O 的直徑為 4,AB 是⊙O 的弦,∠AOB=120°,點 P 在⊙O 上,若點 P到直線 AB 的距離為 1,則∠PAB 的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
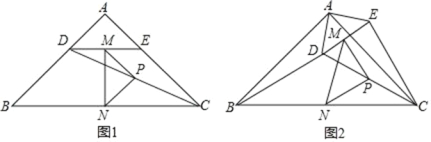
【題目】如圖 1,在 Rt△ABC 中,∠A=90°,AB=AC,點 D、E 分別在邊 AB、AC 上,AD=AE,連接DC,點 M、P、N 分別為 DE、DC、BC 的中點,
(1)觀察猜想:如圖 1 中,△PMN 是 三角形;
(2)探究證明:把△ADE 繞點 A 逆時針方向旋轉到圖 2 的位置,連接 MN,BD, CE.判斷△PMN 的形狀,并說明理由;
(3)拓展延伸:將△ADE 繞點 A 在平面內自由旋轉,若 AD=4,AB=10,請求△PMN 面積的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
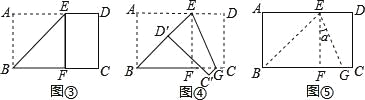
【題目】將長方形紙片 ABCD 沿過點 B 的直線折疊,使點 A 落在 BC 邊上的點 F 處, 折痕為 BE(如圖③);再沿過點 E 的直線折疊,使點 D 落在 BE 上的點處 D′,折痕為 EG(如圖④);再展平紙片(如圖⑤),則圖⑤中∠α=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一塊直角三角形紙片,兩直角邊AB=6,BC=8,將△ABC折疊,使AB落在斜邊AC上,折痕為AD,則BD的長為( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com