Question

已知多項式x²＋ax²＋bx＋c中，a，b，c為常數，當x=1時，多項式的值是1；當x=2時，多項式的值是2；若當x是8和－5時，多項式的值分別為M與N，求M－N的值．

Answer 1

解法1：當x=1時，1＋a＋b＋c=1，

∴a＋b＋c=0．   ①

當x=2時，8＋4a＋2b＋c=2，

∴4a＋2b＋c=－6 ②

聯立①，②解得

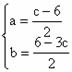
當x=8時，M=512＋64a＋8b＋c，

當x=5時，N=－125＋25a－5b＋c．

∴M－N

=512＋64a＋8b＋c－(－125＋25a－5b＋c)

=637＋39a＋13b

=637－117＋39

=559．

解法2：同解法1得

M=512＋64a＋8b＋c，N=－125＋25a－5b＋c．

M－N=637＋39a＋13b．

由②－①得3a＋b=－6，

∴M－N=637＋13（3a＋b）=637－78=559．

解法3：設P（x）=x³＋ax²＋bx＋c

則P（1）=1，P（2）=2．

又設Q（x）=P（x）－x，

則Q（1）=0，Q（2）=0．

∵Q（x）是關于x的三次多項式，可設Q（x）=（x－1）（x－2）（x－m），其中m為常數．

于是M－N=P（8）－P（－5）

=[Q（8）＋8]－[Q（－5）＋（－5）]

=Q（8）－Q（－5）＋13

=7.6（8－m）－（－6）·（－7）(－5－m)＋13

=336－42m＋210＋42m＋13=559．