
���}Ŀ��ij��˾ُ�M(j��n)ij�Nˮ���ijɱ���![]() Ԫ/ǧ�ˣ���(j��ng)�^�Ј�(ch��ng)�{(di��o)�аl(f��)�F(xi��n)���@�Nˮ����δ��
Ԫ/ǧ�ˣ���(j��ng)�^�Ј�(ch��ng)�{(di��o)�аl(f��)�F(xi��n)���@�Nˮ����δ��![]() ����N�ۃr(ji��)��
����N�ۃr(ji��)��![]() ��Ԫ/ǧ�ˣ��c�r(sh��)�g
��Ԫ/ǧ�ˣ��c�r(sh��)�g![]() ���죩֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��
���죩֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��
 ���������N����
���������N����![]() ��ǧ�ˣ��c�r(sh��)�g
��ǧ�ˣ��c�r(sh��)�g![]() ���죩���P(gu��n)ϵ���±���
���죩���P(gu��n)ϵ���±���
�r(sh��)�g |
|
|
|
|
|
| �� |
���N���� |
|
|
|
|
|
| �� |
![]() ��֪
��֪![]() �c
�c![]() ֮�g��׃��Ҏ(gu��)�ɷ���һ�κ���(sh��)�P(gu��n)ϵ��ԇ���ڵ�
֮�g��׃��Ҏ(gu��)�ɷ���һ�κ���(sh��)�P(gu��n)ϵ��ԇ���ڵ�![]() ������N�����Ƕ��٣�
������N�����Ƕ��٣�
![]() ����һ����N���������������N����������٣�
����һ����N���������������N����������٣�
![]() �ڌ�(sh��)�H�N�۵�ǰ
�ڌ�(sh��)�H�N�۵�ǰ![]() ���У���˾�Q��ÿ�N��
���У���˾�Q��ÿ�N��![]() ǧ��ˮ���;�ٛ(z��ng)
ǧ��ˮ���;�ٛ(z��ng)![]() Ԫ����
Ԫ����![]() �o������(zh��n)��ؚ����(du��)�F(xi��n)�l(f��)�F(xi��n)����ǰ
�o������(zh��n)��ؚ����(du��)�F(xi��n)�l(f��)�F(xi��n)����ǰ![]() ���У�ÿ��۳���ٛ(z��ng)������N�������S�r(sh��)�g
���У�ÿ��۳���ٛ(z��ng)������N�������S�r(sh��)�g![]() �������������
�������������![]() ��ȡֵ������
��ȡֵ������
���𰸡�(1) �ڵ�![]() ������N������
������N������![]() ��(2) ��
��(2) ��![]() ������������������
������������������![]() Ԫ��(3)
Ԫ��(3)![]() ��
��
��������
(1)����(j��)���N����y�c�r(sh��)�gt���P(gu��n)ϵ�����O(sh��)y��kt��b�������Д�(sh��)ֵ���뼴�����һ�κ���(sh��)����ʽ���ٌ�t ��30����һ�κ���(sh��)�Ľ���ʽ�У����������30������N����(2)������(�ۃr(ji��)���ɱ�)���N��������1��t��24��25��t��48�ɷN��r�������}Ŀ�o�����ۃr(ji��)�͕r(sh��)�g֮�g�ĺ���(sh��)�P(gu��n)ϵʽ�քe�ó��N���������P(gu��n)ϵʽ����ͨ�^���κ���(sh��)�D������|(zh��)����������ֵ�����^�ó��Y(ji��)����(3)����(j��)�}���г��P(gu��n)�������Ķ��κ���(sh��)���õ����κ���(sh��)���_�����£���(du��)�Q�S��t��2n��10�Ē��タ��Ҫʹ�����St����������t2n��10��24�����ɵó�n��ȡֵ����.
![]() �O(sh��)
�O(sh��)![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����õ���
����õ���
![]() ��
��
��ã�![]() ��
��
��![]() ��
��
��![]() ������ʽ���ã�
������ʽ���ã�![]() ��
��
�����ڵ�![]() ������N������
������N������![]() ��
��
![]() �O(sh��)��
�O(sh��)��![]() ����N��������
����N��������![]() Ԫ��
Ԫ��
��(d��ng)![]() �r(sh��)�����}��
�r(sh��)�����}��![]() ��
��
��![]() �r(sh��)
�r(sh��)![]() ���ֵ��
���ֵ��![]() Ԫ��
Ԫ��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��
����(du��)�Q�S![]() ��
��![]() ��
��
���ڌ�(du��)�Q�S���(c��)![]() �S
�S![]() ������p��
������p��
��![]() �r(sh��)��
�r(sh��)��![]() ���ֵ
���ֵ![]() ��
��
�C��������![]() ������������������
������������������![]() Ԫ��
Ԫ��
![]() �O(sh��)ÿ��۳���ٛ(z��ng)������N��������
�O(sh��)ÿ��۳���ٛ(z��ng)������N��������![]() Ԫ��
Ԫ��
���}�� ��
��
����ǰ![]() ���У�ÿ��۳���ٛ(z��ng)������N�������S�r(sh��)�g
���У�ÿ��۳���ٛ(z��ng)������N�������S�r(sh��)�g![]() �����������
�����������
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��ȡֵ������
��ȡֵ������![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ABC����(g��)��c(di��n)������(bi��o)�քe��A����2��3����B����6��0����C����1��0����
��1��������ABC�P(gu��n)��y�S��(du��)�Q�ĈD�Ρ�A��B��C�䣬�������c(di��n)A�䡢B'��C�������(bi��o)��
��2���ڈD����һ�c(di��n)D����D��B��C����c(di��n)�������Σ�ʹ���c��ABCȫ�ȣ�Ո(q��ng)�������з��ϗl���ġ�DBC���c(di��n)D�c�c(di��n)A�غϳ��⣩����ֱ�ӌ����c(di��n)D������(bi��o)������ʾ����(d��ng)�c(di��n)D��Ψһ�r(sh��)������D1��D2��D3�ȼ��ԅ^(q��)�e��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���P(gu��n)�� x �ķ��� 2x2+kx��1=0��
��1�����C�������Ѓɂ�(g��)����ȵČ�(sh��)��(sh��)����
��2�������̵�һ��(g��)���ǩ�1������һ��(g��)���� k ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����D����ABC�У�AD�Ǹߣ�AEƽ�֡�BAC����B��50������C��80��.���DAE�ĶȔ�(sh��).

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �鳣��(sh��)���ĈD����D��ʾ������
�鳣��(sh��)���ĈD����D��ʾ������![]() ��(g��)�Y(ji��)Փ����
��(g��)�Y(ji��)Փ����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() �鳣��(sh��)����
�鳣��(sh��)����![]() ���������_�ĽY(ji��)Փ�У� ��
���������_�ĽY(ji��)Փ�У� ��

A. 2��(g��) B. 3��(g��) C. 4��(g��) D. 5��(g��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����о����Ɔ��}�r(sh��)���ס���ͬ�W(xu��)���^�c(di��n)���£�
�ף���߅�L��3��4��5�������ΰ��D1�ķ�ʽ����U(ku��)�����õ��������Σ������Č�(du��)��(y��ng)߅�g����1���t���������cԭ���������ƣ�
�ң�����߅��3��5�ľ��ΰ��D2�ķ�ʽ����U(ku��)�����õ��µľ��Σ������Č�(du��)��(y��ng)߅�g�����1���t�¾����cԭ���β����ƣ�
��(du��)�ڃ��˵��^�c(di��n)�������f�����_���ǣ� ��

A. ���˶���(du��) B. ���˶�����(du��) C. ��(du��)���Ҳ���(du��) D. �ײ���(du��)���Ҍ�(du��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����Rt��ABC�У���C=90����������C��ʹ�c(di��n)C����б߅AB��ijһ�c(di��n)D̎���ۺ۞�EF���c(di��n)E��F�քe��߅AC��BC�ϣ�
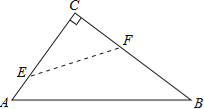
��1������CEF�c��ABC���ƣ�
����(d��ng)AC=BC=2�r(sh��)��AD���L���� ����
����(d��ng)AC=3��BC=4�r(sh��)��AD���L���� ����
��2����(d��ng)�c(di��n)D��AB�����c(di��n)�r(sh��)����CEF�c��ABC���ƆՈ(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ABC=��ACB��AD��BD�քeƽ����ABC����ǡ�EAC����(n��i)�ǡ�ABC�����½Y(ji��)Փ���� AD��BC���ڡ�ACB=2��ADB���� BD��AC���� AC=AD���������_�ĽY(ji��)Փ�У�������

A.�٢�B.�٢ڢ�C.�٢ڢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ֱ��![]() �cֱ��
�cֱ��![]() ������?c��)�ͬһ��(g��)����(bi��o)ϵ�еĈD����£� ����
������?c��)�ͬһ��(g��)����(bi��o)ϵ�еĈD����£� ����
A.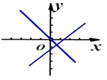 B.
B.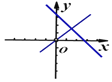
C.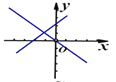 D.
D.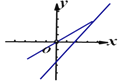
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com