
 與
與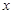 軸交于A、B兩點(點A在點B左側(cè)),與y軸交于點C,且當
軸交于A、B兩點(點A在點B左側(cè)),與y軸交于點C,且當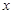 =O和
=O和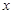 =4時,y的值相等。直線y=4x-16與這條拋物線相交于兩點,其中一點的橫坐標是3,另一點是這條拋物線的頂點M。
=4時,y的值相等。直線y=4x-16與這條拋物線相交于兩點,其中一點的橫坐標是3,另一點是這條拋物線的頂點M。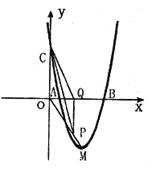
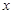 軸于點Q。若點P在線段OM上運動(點P不與點O重合,但可以與點M重合),設OQ的長為t,四邊形PQCO的面積為S,求S與t之間的函數(shù)關系式及自變量t的取值范圍;
軸于點Q。若點P在線段OM上運動(點P不與點O重合,但可以與點M重合),設OQ的長為t,四邊形PQCO的面積為S,求S與t之間的函數(shù)關系式及自變量t的取值范圍;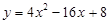 (2)S=2t2+4t,
(2)S=2t2+4t, <
<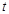 ≤
≤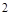 (3)點
(3)點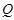 在線段
在線段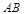 的中點上,16,平行四邊形(4)
的中點上,16,平行四邊形(4)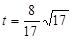
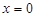 和
和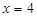 時,
時,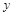 的值相等,∴
的值相等,∴ ,……1分
,……1分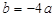 ,∴
,∴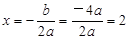
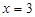 代入
代入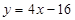 ,得
,得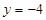 ,
,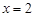 代入
代入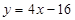 ,得
,得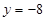 ………………………………………….2分
………………………………………….2分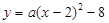
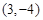 代入,得
代入,得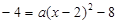 ,解得
,解得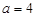 .
.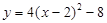 ,即
,即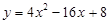 ……………………………..3分
……………………………..3分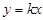 ,將點M
,將點M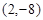 代入,得
代入,得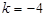 ,
,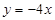 ……………………………………………………………………..4分
……………………………………………………………………..4分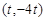 ,
,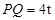 ,而
,而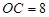 ,
,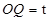 .
.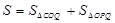 =
=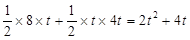 .......................5分
.......................5分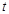 的取值范圍為:
的取值范圍為: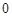 <
<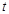 ≤
≤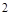 .......................................6分
.......................................6分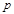 的運動,四邊形
的運動,四邊形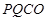 的面積
的面積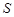 有最大值.
有最大值.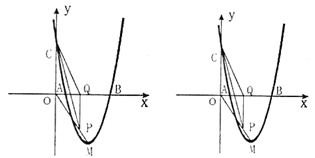
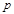 由
由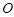 →
→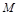 運動,
運動,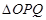 的面積與
的面積與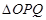 的面積在不斷增大,即
的面積在不斷增大,即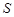 不斷變大,顯當然點
不斷變大,顯當然點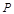 運動到點
運動到點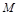 時,
時,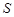 有最值...............7分
有最值...............7分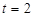 時,點
時,點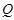 在線段
在線段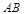 的中點上............. ................8分
的中點上............. ................8分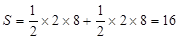 .
.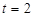 時,
時,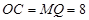 ,
,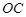 ∥
∥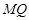 ,∴四邊形
,∴四邊形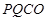 是平行四邊形. ..9分
是平行四邊形. ..9分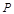 的運動,存在
的運動,存在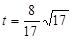 ,能滿足
,能滿足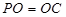 .................10分
.................10分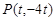 ,
,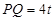 ,
,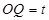 . 由勾股定理,得
. 由勾股定理,得 .
.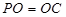 ,∴
,∴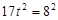 ,
,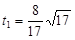 <
<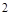 ,
,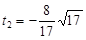 (不合題意)
(不合題意)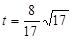 時,
時,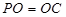 ...................................11分
...................................11分

 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源:不詳 題型:解答題
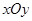 中,半徑為1的圓的圓心
中,半徑為1的圓的圓心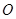 在坐標原點,且與兩坐標軸分別交于
在坐標原點,且與兩坐標軸分別交于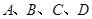 四點.拋物線
四點.拋物線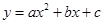 與
與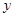 軸交于點
軸交于點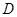 ,與直線
,與直線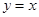 交于點
交于點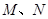 ,且
,且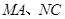 分別與圓
分別與圓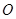 相切于點
相切于點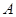 和點
和點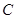 .
.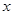 軸于點
軸于點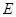 ,連結
,連結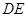 ,并延長
,并延長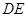 交圓
交圓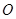 于
于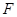 ,求
,求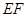 的長.
的長.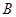 作圓
作圓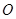 的切線交
的切線交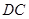 的延長線于點
的延長線于點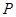 ,判斷點
,判斷點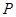 是否在拋物線上,說明理由.
是否在拋物線上,說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:解答題
 的二次函數(shù)
的二次函數(shù) 與
與 ,當
,當 時,
時, ;且二次函數(shù)
;且二次函數(shù) 的圖象的對稱軸是直線
的圖象的對稱軸是直線 .
. 的值;
的值; 的表達式;
的表達式; 的圖象與
的圖象與 的圖象是否有交點?請說明理由.
的圖象是否有交點?請說明理由.查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:解答題

 軸上是否存在點P,使得以P、A、C為頂點的三角形與△BCD相似?若存在,直接寫出點P的坐標;若不存在,請說明理由.
軸上是否存在點P,使得以P、A、C為頂點的三角形與△BCD相似?若存在,直接寫出點P的坐標;若不存在,請說明理由.查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com