
【題目】如圖1,在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過
經過![]() 三點,且其對稱軸為
三點,且其對稱軸為![]() 其中點
其中點![]() ,點
,點![]() .
.
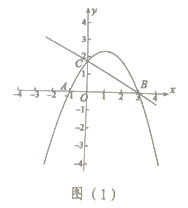
(1)求拋物線的解析式;
(2)①如圖(1),點![]() 是直線
是直線![]() 上方拋物線上的動點,當四邊形
上方拋物線上的動點,當四邊形![]() 的面積取最大值時,求點
的面積取最大值時,求點![]() 的坐標;
的坐標;
②如圖(2),連接![]() 在拋物線上有一點
在拋物線上有一點![]() 滿足
滿足![]() ,請直接寫出點
,請直接寫出點![]() 的橫坐標.
的橫坐標.
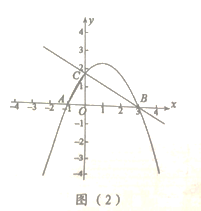
【答案】(1)![]() ;(2)①D
;(2)①D ,②
,②![]() 或
或![]()
【解析】
(1)根據點![]() ,點
,點![]() ,利用待定系數法,可得函數解析式;
,利用待定系數法,可得函數解析式;
(2)①先求出直線BC的解析式,當直線m與拋物線只有一個交點時,點D到BC的距離最遠,此時△BCD取最大值,故四邊形DCAB有最大值,求出b的值代入原式即可得到答案;
②根據題干條件拋物線上有一點![]() 滿足
滿足![]() ,通過利用待定系數法利用方程組求出直線BE的解析式,可得答案.
,通過利用待定系數法利用方程組求出直線BE的解析式,可得答案.
解:(1)由題意得:
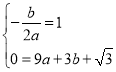
解得![]()
故拋物線的解析式是![]() .
.


圖(1) 圖(2)
(2)①設直線BC的解析式為y=kx+![]() .
.
∵直線BC過點B(3,0),
∴0=3k+![]()
則k=![]() ,
,
故直線BC解析式為y=![]() x+
x+![]() .
.
設直線m解析式為![]() ,且直線m∥直線BC
,且直線m∥直線BC
當直線m與拋物線只有一個交點時,點D到BC的距離最遠,此時△BCD取最大值,故四邊形DCAB有最大值.
令![]() ,
,
![]()
當![]() 時
時
直線m與拋物線有唯一交點
解之得:![]()
代入原式可求得:![]()
∴D![]()
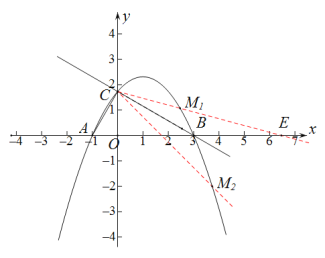
圖(3)
過D作DP∥y軸交CB于點P,△DCB面積=△DPC面積+△DPB面積,
∴D
②存在,點M的橫坐標為![]() 或
或![]()
解題提示:如圖3
符合條件的直線有兩條: CM1和CM2(分別在CB的上方和下方)
∵在Rt△ACO中,∠ACO=30°,在Rt△COB中,∠CBO=30°,
∴∠BCM1=∠BCM2=15°
∵△BCE中,∠BCE=∠BEC2=15°
∴BC=BE=![]()
則E(![]() ,0)
,0)
設直線CE解析式為:![]()
∴![]()
解之得:k=![]()
∴直線CE解析式為:![]()
∴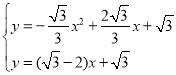
解得:x1=0,x2=2![]() -1
-1
∵ 在Rt△OCF中,∠CBO=30°,∠BCF=15°
∴在Rt△COF中, ∠CFO=45°
∴OC=OF=![]()
∴F(![]() ,0)
,0)
∴直線CF的解析式為![]()
∴
解之得:![]() (舍去),
(舍去),![]()
即點M的橫坐標為:![]() 或
或![]()


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD,AB=6,點E在邊CD上,CE=2DE,將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG、CF,下列結論:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正確結論是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某地區企業信息化發展水平,從該地區中隨機抽取50家企業調研,針對體現企業信息化發展水平的A和B兩項指標進行評估,獲得了它們的成績(十分制),并對數據(成績)進行整理、描述和分析.下面給出了部分信息.
a.A項指標成績的頻數分布直方圖如下(數據分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
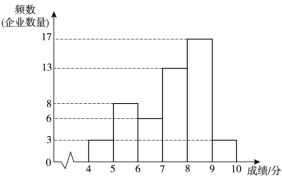
b.A項指標成績在![]() 這一組的是:
這一組的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 兩項指標成績的平均數、中位數、眾數如下:
兩項指標成績的平均數、中位數、眾數如下:
平均數 | 中位數 | 眾數 | |
A項指標成績 | 7.37 | m | 8.2 |
B項指標成績 | 7.21 | 7.3 | 8 |
根據以上信息,回答下列問題:
(1)寫出表中m的值
(2)在此次調研評估中,某企業A項指標成績和B項指標成績都是7.5分,該企業成績排名更靠前的指標是______________(填“A”或“B”),理由是_____________;
(3)如果該地區有500家企業,估計A項指標成績超過7.68分的企業數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O上依次有A、B、C三點,BO的延長線交⊙O于E,![]() ,過點C作CD∥AB交BE的延長線于D,連AD交⊙O于點F.
,過點C作CD∥AB交BE的延長線于D,連AD交⊙O于點F.
(1)求證:四邊形ABCD是菱形;
(2)連接OA、OF.
①當∠ABC= °時,點F為![]() 的中點;
的中點;
②若∠AOF=3∠FOE且AF=3,則⊙O的半徑是 .
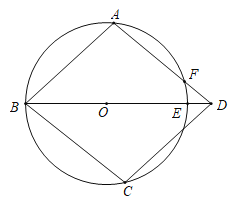
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把某矩形紙片ABCD沿EF、GH折疊(點E、H在AD邊上,點F、G在BC邊上),使得點B、點C落在AD邊上同一點P處,A點的對稱點為![]() 點,D點的對稱點為
點,D點的對稱點為![]() 點,若
點,若![]() ,
,![]() 的面積為4,
的面積為4,![]() 的面積為1,則矩形ABCD的面積等于_____.
的面積為1,則矩形ABCD的面積等于_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場服裝部為了調動營業員的積極性,決定實行目標管理,根據目標完成的情況對營業員進行適當的獎勵.為了確定一個適當的月銷售目標,商場服裝部統計了每位營業員在某月的銷售額(單位:萬元),數據如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
對這30個數據按組距3進行分組,并整理、描述和分析如下:
頻數分布表
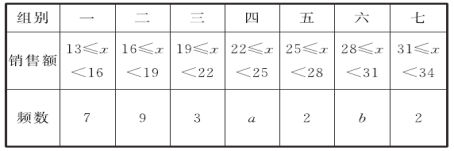
數據分析表
平均數 | 眾數 | 中位數 |
20.3 | c | 18 |
請根據以上信息解答下列問題:
(1)填空:a=____,b=_____,c=_____;
(2)若將月銷售額不低于25萬元確定為銷售目標,則有______位營業員獲得獎勵;
(3)若想讓一半左右的營業員都能達到銷售目標,你認為月銷售額定為多少合適?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對垃圾進行分類投放,能提高垃圾處理和再利用的效率,減少污染,保護環境.為了檢查垃圾分類的落實情況,某居委會成立了甲、乙兩個檢查組,采取隨機抽查的方式分別對轄區內的A,B,C,D四個小區進行檢查,并且每個小區不重復檢查.
(1)甲組抽到A小區的概率是多少;
(2)請用列表或畫樹狀圖的方法求甲組抽到A小區,同時乙組抽到C小區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,隨機選取該校部分學生進行調查,要求每名學生從中選出一類最喜愛的電視節目,以下是根據調查結果繪制的統計圖表的一部分.
類別 |
|
|
|
|
|
類型 | 新聞 | 體育 | 動畫 | 娛樂 | 戲曲 |
人數 | 11 | 20 | 40 |
| 4 |
請你根據以上信息,回答下列問題:
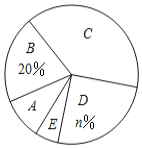
(1)統計表中![]() 的值為_______,統計圖中
的值為_______,統計圖中![]() 的值為______,
的值為______,![]() 類對應扇形的圓心角為_____度;
類對應扇形的圓心角為_____度;
(2)該校共有1500名學生,根據調查結果,估計該校最喜愛體育節目的學生人數;
(3)樣本數據中最喜愛戲曲節目的有4人,其中僅有1名男生.從這4人中任選2名同學去觀賞戲曲表演,請用樹狀圖或列表求所選2名同學中有男生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com