
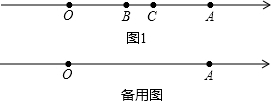
分析 (1)由題意可知B點表示的數比點C對應的數少3,進一步用b表示出AC、OB之間的距離,聯立方程求得b的數值即可;
(2)分別用b表示出AC、OB、AB,進一步利用AC-0B=$\frac{1}{2}$AB建立方程求得答案即可.
解答 解:(1)由題意得:
11-(b+3)=b,
解得:b=4.
答:線段AC=OB,此時b的值是4.
(2)由題意得:
①11-(b+3)-b=$\frac{1}{2}$(11-b),
解得:b=$\frac{5}{3}$.
②11-(b+3)+b=$\frac{1}{2}$(11-b),
解得:b=-5.
答:若AC-0B=$\frac{1}{2}$AB,滿足條件的b值是$\frac{5}{3}$或-5.
點評 本題考查了一元一次方程的應用,考查了數軸與兩點間的距離的計算,根據數軸確定出線段的長度是解題的關鍵.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:解答題
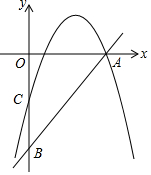 如圖,直線y=2x-10分別與x軸,y軸交于點A,B,點C為OB的中點,拋物線y=-x2+bx+c經過A,C兩點.
如圖,直線y=2x-10分別與x軸,y軸交于點A,B,點C為OB的中點,拋物線y=-x2+bx+c經過A,C兩點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 我愛美 | B. | 中華游 | C. | 愛我中華 | D. | 美我中華 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x-1)-2(2+3x)=13 | B. | (x-1)+2(2x+3)=1 | C. | 3(x-1)+2(2+3x)=6 | D. | 3(x-1)-2(2x+3)=6 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{27}$÷$\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
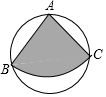 如圖,從直徑是2米的圓形鐵皮上剪出一個圓心角是90°的扇形ABC(A,B,C三點在⊙O上),將剪下來的扇形圍成一個圓錐的側面,則該圓錐的底面圓的半徑為( )
如圖,從直徑是2米的圓形鐵皮上剪出一個圓心角是90°的扇形ABC(A,B,C三點在⊙O上),將剪下來的扇形圍成一個圓錐的側面,則該圓錐的底面圓的半徑為( )| A. | 4-$\frac{π}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 為檢測市場上正在銷售的酸奶質量,應該采用全面調查的方式 | |
| B. | 在連續5次的數學測試中,兩名同學的平均分相同,方差較大的同學數學成績更穩定 | |
| C. | 小強班上有3個同學都是16歲,因此小強認為他們班學生年齡的眾數是16歲 | |
| D. | 給定一組數據,則這組數據的中位數一定只有一個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com