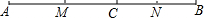Question

9．如圖．點C是線段AB上一點，點M．N分別是線段AC、BC的中點．
（1）若線段AC=6，BC=4，求線段MN的長；
（2）若AC+BC=a，求線段MN的長；
（3）題目中“點C是線段AB上”，若改為“點C是直線AB上”，（1）中結果會變嗎？若有變．請求線段MN的長．

Answer 1

分析 （1）根據點M、N分別是AC、BC的中點，先求出CM、CN的長度，則MN=CM+CN；
（2）根據點M、N分別是AC、BC的中點，CM=$\frac{1}{2}$AC，CN=$\frac{1}{2}$BC，所以MN=$\frac{1}{2}$（AC+BC）=$\frac{a+b}{2}$；
（3）長度會發生變化，分點C在線段AB上、點B在A、C之間和點A在B、C之間三種情況討論．

解答 解：（1）∵AC=6，點M是AC的中點
∴CM=$\frac{1}{2}$AC=3cm
∵BC=4，點N是BC的中點
∴CN=$\frac{1}{2}$BC=2，
∴MN=CM+CN=5，
∴線段MN的長度為5．

（2）MN=$\frac{a+b}{2}$．

（3）線段MN的長度會變化．
當點C在線段AB上時，由（2）知MN=$\frac{a+b}{2}$，
當點C在線段AB的延長線時，如圖1：

則AC=a＞BC=b，
∵AC=a點M是AC的中點，
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$a，
∵BC=b點N是BC的中點
∴CN=$\frac{1}{2}$BC=$\frac{1}{2}$b，
∴MN=CM-CN=$\frac{a-b}{2}$，
當點C在線段BA的延長線時，如圖2：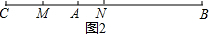
，
則AC=a＜BC=b
同理可求：CM=$\frac{1}{2}$AC=$\frac{1}{2}$a，
CN=$\frac{1}{2}$BC=$\frac{1}{2}$b，
∴MN=CN-CM=$\frac{b-a}{2}$，
綜上所述，線段MN的長度會變化，MN=$\frac{a+b}{2}$，$\frac{a-b}{2}$，$\frac{b-a}{2}$．

點評 本題主要是線段中點的運用，分情況討論是解題的難點，難度較大．