
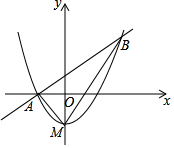
 如圖,頂點M在y軸上的拋物線與直線y=x+1相交于A、B兩點,且點A在x軸上,點B的橫坐標為2,連結AM、BM.
如圖,頂點M在y軸上的拋物線與直線y=x+1相交于A、B兩點,且點A在x軸上,點B的橫坐標為2,連結AM、BM.分析 (1)由條件可分別求得A、B的坐標,設出拋物線解析式,利用待定系數法可求得拋物線解析式;
(2)結合(1)中A、B、C的坐標,根據勾股定理可分別求得AB、AM、BM,可得到AB2+AM2=BM2,可判定△ABM為直角三角形.
解答 解:(1)∵A點為直線y=x+1與x軸的交點,
∴A(-1,0),
又B點橫坐標為2,代入y=x+1可求得y=3,
∴B(2,3),
∵拋物線頂點在y軸上,
∴可設拋物線解析式為y=ax2+c,
把A、B兩點坐標代入可得$\left\{\begin{array}{l}{a+c=0}\\{4a+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{c=-1}\end{array}\right.$,
∴拋物線解析式為y=x2-1;
(2)△ABM為直角三角形.理由如下:
由(1)拋物線解析式為y=x2-1,可知M點坐標為(0,-1),
∴AM2=12+12=2,AB2=(2+1)2+32=18,BM2=22+(3+1)2=20,
∴AM2+AB2=2+18=20=BM2,
∴△ABM為直角三角形.
點評 本題考查了待定系數法求二次函數的解析式,二次函數的性質,勾股定理及其逆定理等知識點.在(1)中確定出A、B兩點的坐標是解題的關鍵,在(2)中分別求得AB、AM、BM的長是解題的關鍵.本題考查知識點較為基礎,難度適中.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:初中數學 來源: 題型:選擇題
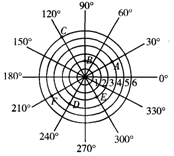 如圖,雷達探測器測得六個目標A,B,C,D,E,F出現按照規定的目標表示方法,目標E,F的位置表示為E(3,300°),F(5,210°),按照此方法在表示目標A,B,D,E的位置時,其中表示不正確的是( )
如圖,雷達探測器測得六個目標A,B,C,D,E,F出現按照規定的目標表示方法,目標E,F的位置表示為E(3,300°),F(5,210°),按照此方法在表示目標A,B,D,E的位置時,其中表示不正確的是( )| A. | A(4,30°) | B. | B(2,90°) | C. | C(6,120°) | D. | D(3,240°) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 86×102 | B. | 8.6×103 | C. | 86×103 | D. | 0.86×103 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 實驗的麥種數/粒 | 500 | 500 | 500 | 500 | 500 |
| 發芽的麥種數/粒 | 492 | 487 | 491 | 493 | 489 |
| 發芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 ∠ACB=∠ADC=90°,AC=3,CD=2.當AB的長為$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$時,這兩個直角三角形相似.
∠ACB=∠ADC=90°,AC=3,CD=2.當AB的長為$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$時,這兩個直角三角形相似.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com