
【題目】在平面直角坐標系第一象限中,已知點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,動點
,動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度勻速向點
個單位長度的速度勻速向點![]() 方向運動,與此同時,
方向運動,與此同時,![]() 軸上動點
軸上動點![]() 從點
從點![]() 出發,以相同的速度向右運動, 兩動點運動時間為:
出發,以相同的速度向右運動, 兩動點運動時間為:![]() , 以
, 以![]() 分別為邊作矩形
分別為邊作矩形![]() , 過點
, 過點![]() 作雙曲線交線段
作雙曲線交線段![]() 于點
于點![]() ,作
,作![]() 中點
中點![]() ,連接
,連接![]()
(1)當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
(2)若![]() 平分
平分![]() , 則
, 則![]() 的值為多少?
的值為多少?
(3)若![]() 為直角, 則
為直角, 則![]() 的值為多少?
的值為多少?

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 時,E點的坐標,然后求出雙曲線的解析式,進而可求出F點的坐標;
時,E點的坐標,然后求出雙曲線的解析式,進而可求出F點的坐標;
(2)先求出E點的坐標,然后求出雙曲線的解析式,進而可求出F點的坐標,然后利用角平分線的定義和平行線的性質得出![]() ,即可求出t的值;
,即可求出t的值;
(3)延長EM,BC交于點N,先求出E點的坐標,然后求出雙曲線的解析式,進而可求出F點的坐標,然后通過平行線的性質和中點得出![]() ,則有
,則有![]() ,進而得出
,進而得出![]() ,然后再證明
,然后再證明![]() ,得出
,得出![]() ,從而建立一個關于t的方程,解方程求解即可.
,從而建立一個關于t的方程,解方程求解即可.
(1)當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
設雙曲線的解析式為![]() ,
,
將點E代入解析式中,有![]() ,
,
∴雙曲線的解析式為![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
∴當![]() 時,
時,![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() .
.
設雙曲線的解析式為![]() ,
,
將點E代入解析式中,有![]() ,
,
∴雙曲線的解析式為![]() ,
,
∴當![]() 時,
時,![]() ,
,
![]() .
.
∵BE平分![]() ,
,
![]() .
.
∵四邊形ABCD為矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
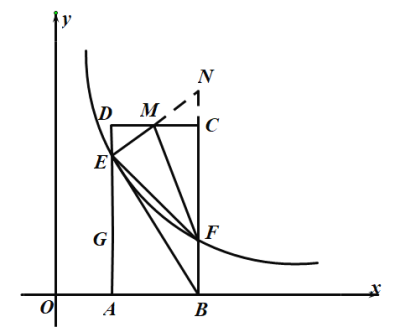
(3)延長EM,BC交于點N,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴![]() .
.
設雙曲線的解析式為![]() ,
,
將點E代入解析式中,有![]() ,
,
∴雙曲線的解析式為![]() ,
,
∴當![]() 時,
時,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵點M為CD中點,
∴![]() .
.
在![]() 和
和![]() 中,
中,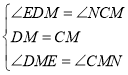
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() 為直角,
為直角,
![]() ,
,
在![]() 和
和![]() 中,
中,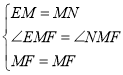
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】為支援雅安災區,某學校計劃用“義捐義賣”活動中籌集的部分資金用于購買A,B兩種型號的學習用品共1000件,已知A型學習用品的單價為20元,B型學習用品的單價為30元.
(1)若購買這批學習用品用了26000元,則購買A,B兩種學習用品各多少件?
(2)若購買這批學習用品的錢不超過28000元,則最多購買B型學習用品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=3,AC=4,BC=5,P 為邊 BC 上一動點,PE⊥AB 于 E,PF⊥AC于 F,M 為 EF 中點,則 AM 的最小值為( )
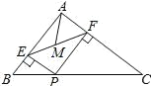
A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中數學 來源: 題型:
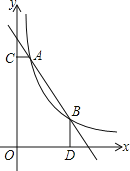
【題目】如圖,一次函數![]() 與函數
與函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,
兩點,![]() 軸于C,
軸于C,![]() 軸于D
軸于D
![]() 求k的值;
求k的值;
![]() 根據圖象直接寫出
根據圖象直接寫出![]() 的x的取值范圍;
的x的取值范圍;
![]() 是線段AB上的一點,連接PC,PD,若
是線段AB上的一點,連接PC,PD,若![]() 和
和![]() 面積相等,求點P坐標.
面積相等,求點P坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
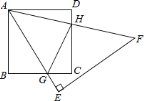
【題目】如圖,正方形ABCD的面積為1cm2,△AEF為等腰直角三角形,∠E=90°,AE和BC交于點G,AF和CD交于點H,則△CGH的周長_________
查看答案和解析>>
科目:初中數學 來源: 題型:
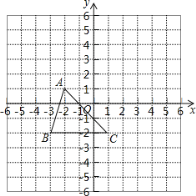
【題目】如圖所示,三角形![]() 記作
記作![]() 在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,先將
在方格中,方格紙中的每個小方格都是邊長為1個單位的正方形,先將![]() 向上平移3個單位長度,再向右平移2個單位長度,得到
向上平移3個單位長度,再向右平移2個單位長度,得到![]() .
.
![]() 三個頂點的坐標分別是:
三個頂點的坐標分別是:![]() ______
______![]() ,
,![]() ______
______![]() ,
,![]() ______
______![]() ,
,
![]() 在圖中畫出
在圖中畫出![]() ;
;
![]() 平移后
平移后![]() 的三個頂點坐標分別為:
的三個頂點坐標分別為:![]() ______
______![]() 、
、![]() ______
______![]() 、
、![]() ______
______![]() ;
;
![]() 若y軸有一點P,使
若y軸有一點P,使![]() 與
與![]() 面積相等,則P點的坐標為______.
面積相等,則P點的坐標為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知甲、乙兩站的路程是312km,一列列車從甲站開往乙站,設列車的平均速度為xkm/h,所需時間為yh.
(1)試寫出y關于x的函數關系式;
(2)2006年全國鐵路第六次大提速前,這列列車從甲站到乙站需要4h,列車提速后,速度提高了26km/h,問提速后從甲站到乙站需要幾個小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
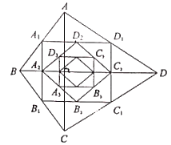
【題目】如圖,四邊形![]() 中,
中,![]() 順次連接四邊形
順次連接四邊形![]() 各邊中點,得到四邊形
各邊中點,得到四邊形![]() ,再順次連接四邊形
,再順次連接四邊形![]() 各邊中點,得到四邊形
各邊中點,得到四邊形![]() ...如此進行下去,得到四邊形
...如此進行下去,得到四邊形![]() 則下列結論正確的個數有( )
則下列結論正確的個數有( )
①四邊形![]() 是矩形;②四邊形
是矩形;②四邊形![]() 是菱形;③四邊形
是菱形;③四邊形![]() 的周長為
的周長為![]() ; ④四邊形
; ④四邊形![]() 的面積是
的面積是![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
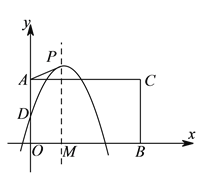
【題目】如圖,在平面直角坐標系中,點![]() ,
, ![]() 分別是
分別是![]() 軸正半軸,
軸正半軸, ![]() 軸正半軸上兩動點,
軸正半軸上兩動點, ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 為鄰邊構造矩形
為鄰邊構造矩形![]() ,拋物線
,拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
, ![]() 為頂點,
為頂點, ![]() 軸于點
軸于點![]() .
.
(![]() )求
)求![]() ,
, ![]() 的長(結果均用含
的長(結果均用含![]() 的代數式表示);
的代數式表示);
(![]() )當
)當![]() 時,求該拋物線的表達式;
時,求該拋物線的表達式;
(![]() )在點
)在點![]() 在整個運動過程中,若存在
在整個運動過程中,若存在![]() 是等腰三角形,請求出所有滿足條件的
是等腰三角形,請求出所有滿足條件的![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com