
【題目】如圖1,射線![]() 在
在![]() 的內部,圖中共有3個角:
的內部,圖中共有3個角:![]() ,
,![]() 和
和![]() ,若其中有一個角的度數是另一個角度數的兩倍,則稱射線
,若其中有一個角的度數是另一個角度數的兩倍,則稱射線![]() 是
是![]() 的奇妙線.
的奇妙線.
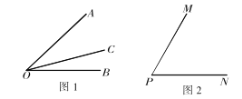
(1)如圖1,在![]() 的內部,
的內部,![]() 有_________條奇妙線;
有_________條奇妙線;
(2)如圖2,若![]() ,射線
,射線![]() 繞點
繞點![]() 從
從![]() 位置開始,以每秒
位置開始,以每秒![]() 的速度逆時針旋轉,當
的速度逆時針旋轉,當![]() 首次等于
首次等于![]() 時停止旋轉,設旋轉的時間為
時停止旋轉,設旋轉的時間為![]() .
.
①直接寫出當![]() 為何值時,射線
為何值時,射線![]() 是
是![]() 的奇妙線?
的奇妙線?
②若射線![]() 同時繞點
同時繞點![]() 以每秒
以每秒![]() 的速度逆時針旋轉,并與
的速度逆時針旋轉,并與![]() 同時停止旋轉.請求出當射線
同時停止旋轉.請求出當射線![]() 是
是![]() 的奇妙線時
的奇妙線時![]() 的值.
的值.
【答案】(1)3;(2)①t為4.5或6或9 ;②![]() 或
或![]() 或
或![]()
【解析】
(1)根據奇妙線的定義,若OC是射線![]() 是
是![]() 的奇妙線,有∠AOB=2∠AOC、∠AOC=2∠BOC、∠BOC=2∠AOC三種情況;
的奇妙線,有∠AOB=2∠AOC、∠AOC=2∠BOC、∠BOC=2∠AOC三種情況;
(2)①表達出∠QPN、∠QPM=20°t-60°,再分三種情況,根據奇妙線的定義列出方程即可求解;
②表達出∠QPN、∠M’PN、∠M’PQ,再分三種情況,根據奇妙線的定義列出方程即可求解;
解:(1)若∠AOB=2∠AOC,則OC是射線![]() 是
是![]() 的奇妙線,
的奇妙線,
若∠AOC=2∠BOC,則OC是射線![]() 是
是![]() 的奇妙線
的奇妙線
若∠BOC=2∠AOC,則OC是射線![]() 是
是![]() 的奇妙線
的奇妙線
∴在![]() 的內部,
的內部,![]() 有3條奇妙線,
有3條奇妙線,
故答案為:3.
(2)①∵∠QPN=20°t,∠MPN=60°
∴∠QPM=20°t-60°
當∠QPN=2∠MPN時,即20°t=120°,解得t=6s,
當∠QPM=2∠MPN時,即20°t-60°=120°,解得t=9s,
當∠MPN=2∠QPM時,即60°=2(20°t-60°),解得t=4.5s,
故答案為:t為4.5或6或9.
②由題意得:∠QPN=20°t,∠M’PN=60°+12°t,∠M’PQ=60°-8°t
當![]() 時
時
∴![]()
∴![]()
當![]() 時,
時,
∴![]()
∴![]()
當![]() 時,
時,
∴![]()
∴![]()
綜上所述,當![]() 或
或![]() 或
或![]() 時,射線
時,射線![]() 是
是![]() 的奇妙線.
的奇妙線.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:初中數學 來源: 題型:
【題目】請根據圖中提供的暖瓶和水杯的售價信息,回答下列問題:
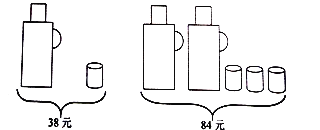
(1)一個暖瓶與一個水杯的售價分別是多少元?
(2)甲、乙兩家商場同時出售同樣的暖瓶和水杯,在新年期間,兩家商場都在搞促銷活動.甲商場規定:這兩種商品都打8.5折;乙商場規定:兩種商品都不打折,但買一個暖瓶贈送一個水杯.若某單位想要買4個暖瓶和16個水杯,請問這個單位選擇哪家商場購買更合算,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按如下規律擺放三角形:
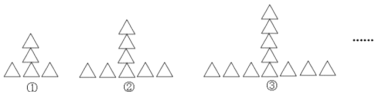
(1)圖④中分別有多少個三角形?
(2)按上述規律排列下去,第n個圖形中有多少個三角形?
(3)按上述規律排列下去,第2014個圖形中有多少個三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題情境)
如圖1,四邊形ABCD是正方形,M是BC邊上的一點,E是CD邊的中點,AE平分∠DAM.求證:AM=AD+MC.

(探究展示)
(2)若四邊形ABCD是長與寬不相等的矩形,其他條件不變,如圖2,試判斷AM=AD+MC是否成立?若成立,請給出證明,若不成立,請說明理由;
(拓展延伸)
(3)若(2)中矩形ABCD兩邊AB=6,BC=9,求AM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2015珠海)閱讀材料:善于思考的小軍在解方程組![]() 時,采用了一種“整體代換”的解法:將方程②變形:4x+10y+y=5 即2(2x+5y)+y=5③
時,采用了一種“整體代換”的解法:將方程②變形:4x+10y+y=5 即2(2x+5y)+y=5③
把方程①帶入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程組的解為![]() .
.
請你解決以下問題:(1)模仿小軍的“整體代換”法解方程組![]() ;
;
(2)已知x,y滿足方程組![]() .
.
(i)求![]() 的值;
的值;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
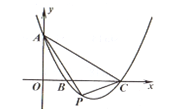
【題目】如圖,平面直角坐標系中,拋物線y=-![]() x2-2x+3交x軸于點B,C,交y軸于點A,點P(x,y)是拋物線上的一個動點,連接PA,AC,PC,記△ACP面積為S.當y≤3時,S隨x變化的圖象大致是( )
x2-2x+3交x軸于點B,C,交y軸于點A,點P(x,y)是拋物線上的一個動點,連接PA,AC,PC,記△ACP面積為S.當y≤3時,S隨x變化的圖象大致是( )
A. 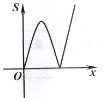 B.
B.  C.
C. 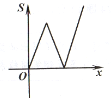 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為深化課改,落實立德樹人目標,某學校設置了以下四門拓展性課程:A.數學思維,B.文學鑒賞,C.紅船課程,D.3D打印,規定每位學生選報一門.為了解學生的報名情況,隨機抽取了部分學生進行調查,并制作成如下兩幅不完整的統計圖,請回答下列問題:
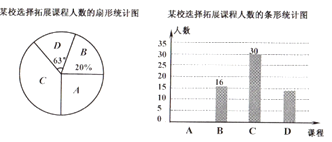
(1)求這次被調查的學生人數;
(2)請將條形統計圖補充完整;
(3)假如全校有學生1000人,請估計選報“紅船課程”的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com