
分析 分類討論:①以OM為底時,點M的個數;②以AM為底時,點M的個數;③以AO為底邊時,點M的個數.
解答 解:因為△AOM為等腰三角形,所以可分成三類討論:
①AO=AM(有一個)
此時只要以A為圓心AO長為半徑畫圓,可知圓與y軸交于O點和另一個點,另一個點就是M;
②AO=OM(有兩個)
此時只要以O為圓心AO長為半徑畫圓,可知圓與y軸交于兩個點,這兩個點就是M的兩種選擇(AO=OM=R)
③AM=OM(一個)
作AO的中垂線,與y軸有一個交點,該交點就是點M的最后一種選擇.(利用中垂線性質)
綜上所述,共有4個.
故答案為:4.
點評 本題考查了等腰三角形的判定及坐標與圖形的性質;解答本題極易漏解,所以解答時,應利用“分類討論”的數學思想.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
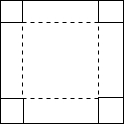 如圖,在邊長為acm的正方形紙片的四角處各剪去邊長為xcm的正方形,然后沿虛線折疊成一個無蓋的長方體盒子,則盒子的容積為a2x-4ax2+4x3cm3,當a=8cm,x=1.5cm時,盒子的容積為37.5cm3.
如圖,在邊長為acm的正方形紙片的四角處各剪去邊長為xcm的正方形,然后沿虛線折疊成一個無蓋的長方體盒子,則盒子的容積為a2x-4ax2+4x3cm3,當a=8cm,x=1.5cm時,盒子的容積為37.5cm3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
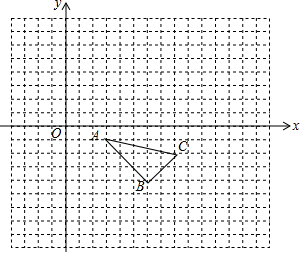 如圖,在平面直角坐標系中,△ABC的頂點坐標分別為(3,-1),(6,-4),(8,-2).
如圖,在平面直角坐標系中,△ABC的頂點坐標分別為(3,-1),(6,-4),(8,-2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
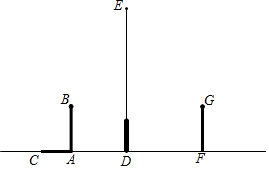 如圖,在路燈下,小明的身高如圖中線段AB所示,他在地面上的影子如圖中線段AC所示,小亮的身高如圖中線段FG所示,路燈燈泡在線段DE上.
如圖,在路燈下,小明的身高如圖中線段AB所示,他在地面上的影子如圖中線段AC所示,小亮的身高如圖中線段FG所示,路燈燈泡在線段DE上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com