
【題目】小南發現操場中有一個不規則的封閉圖形ABC.為了知道它的面積,他在封閉圖形內畫出了一個半徑為1米的圓,在不遠處向圈內擲石子,若石子落在圖形ABC以外,則重擲.記錄如下:
石子落在圓內(含圓上)的次數 | 14 | 43 | 93 | 150 |
石子落在陰影內的次數 | 23 | 91 | 186 | 300 |
根據以上的數據,小南得到了封閉圖形ABC的面積.
請根據以上信息,回答以下問題:
(1)求石子落在圓內(含圓上)的頻率;
(2)估計封閉圖形ABC的面積.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC是一塊銳角三角形材料,高線AH長8 cm,底邊BC長10 cm,要把它加工成一個矩形零件,使矩形DEFG的一邊EF在BC上,其余兩個頂點D,G分別在AB,AC上,則四邊形DEFG的最大面積為( )

A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學之道在于悟,希望同學們在問題(1)解決過程中有所感悟,再繼續探索研究問題(2)(3).
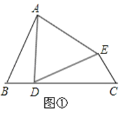
(1)如圖①,D在線段BC上,∠B=∠C=∠ADE,AD=DE.求證:△ABD≌△DCE.
(2)如圖②,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=4,在CB的延長線上有一動點D,連接AD,以AD為直角邊作等腰直角三角形ADE(∠ADE=90°,AD=DE ),連接EB并延長,與AC的延長線交于點F.當動點D在運動過程中,CF的長度是否會發生變化,如果變化,請說明理由;如果不變,請求出CF的長.
(3)如圖③,射線AM與BN,MA⊥AB,NB⊥AB,點P是AB上一點, PA=1,PB=2,在射線AM與BN上分別作點C、點D,滿足△CPD為等腰直角三角形.則△CPD的面積為 .


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 經過某種變換后得到點
經過某種變換后得到點![]() ,我們把點
,我們把點![]()
![]() 叫做點
叫做點![]() 的終結點.已知點
的終結點.已知點![]() 的終結點為
的終結點為![]() ,點
,點![]() 的終結點為
的終結點為![]() ,點
,點![]() 的終結點為
的終結點為![]() ,這樣依次得到
,這樣依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,則點
,則點![]() 的坐標為( )
的坐標為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,BC=2![]() .點P從點A出發沿沿射線AB以1
.點P從點A出發沿沿射線AB以1![]() 的速度運動,過點P作PE∥BC交射線AC于點E,同時點Q從點C出發沿BC的延長線以1
的速度運動,過點P作PE∥BC交射線AC于點E,同時點Q從點C出發沿BC的延長線以1![]() 的速度運動,連結BE、EQ.設點P的運動時間為t(
的速度運動,連結BE、EQ.設點P的運動時間為t(![]() ).
).

(1)求證:△APE是等邊三角形;
(2)直接寫出CE的長(用含![]() 的代數式表示);
的代數式表示);
(3)當點P在邊AB上,且不與點A、B重合時,求證:△BPE≌△ECQ.
(4)在不添加字母和連結其它線段的條件下,當圖中等腰三角形的個數大于3時,直接寫出t的值和對應的等腰三角形的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋擲一枚均勻的骰子(各面上的點數分別為1﹣6點)1次,落地后:
(1)朝上的點數有哪些結果?他們發生的可能性一樣嗎?
(2)朝上的點數是奇數與朝上的點數是偶數,這兩個事件的發生可能性大小相等嗎?
(3)朝上的點數大于4與朝上的點數不大于4,這兩個事件的發生可能性大小相等嗎?如果不相等,那么哪一個可能性大一些?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,□ABCD中,∠ABC為銳角,AB<BC,點E是AD上的一點,延長CE到F,連接BF交AD于點G, 使∠FBC=∠DCE.
⑴ 求證:∠D=∠F;
⑵ 在直線AD找一點P,使以點B、P、C為頂點的三角形與以點C、D、P為頂點的三角形相似.(在原圖中標出準確P點的位置,必要時用直尺和圓規作出P點,保留作圖的痕跡,不寫作法)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() ,
,![]() ,點C為x軸正半軸上一動點,過點A作
,點C為x軸正半軸上一動點,過點A作![]() 交y軸于點E.
交y軸于點E.

![]() 如圖
如圖![]() ,若點C的坐標為
,若點C的坐標為![]() ,試求點E的坐標;
,試求點E的坐標;
![]() 如圖
如圖![]() ,若點C在x軸正半軸上運動,且
,若點C在x軸正半軸上運動,且![]() , 其它條件不變,連接DO,求證:OD平分
, 其它條件不變,連接DO,求證:OD平分![]()
![]() 若點C在x軸正半軸上運動,當
若點C在x軸正半軸上運動,當![]() 時,求
時,求![]() 的度數.
的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com