【答案】
分析:過O作OC垂直于AB,根據垂徑定理可得C為AB的中點,由AB的長求出AC的長,又OA=OB,OC垂直于AB,根據三線合一得到OC為角平分線,根據∠AOB的度數求出∠AOC的度數為60°,根據直角三角形的兩銳角互余可得∠A=30°,可設OC為xcm,根據30°所對的直角邊等于斜邊的一半可得AB=2xcm,再由AC的長,利用勾股定理列出關于x的方程,求出方程的解得到x的值,可得出AB的長,即為圓的半徑.
解答:解:過O作OC⊥AB,垂足為C,如圖所示:
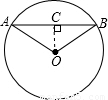
∵OC⊥AB,且AB=2
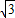
cm,
∴AC=BC=

AB=
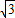
cm,
又∵OA=OB,OC⊥AB,
∴OC為∠AOB的平分線,∠AOB=120°
∴∠AOC=∠BOC=

∠AOB=60°,
在Rt△AOC中,∠ACO=90°,∠AOC=60°,
∴∠A=30°,
設OC=xcm,則有OA=2xcm,
根據勾股定理得:AC
2+OC
2=OA
2,即3+x
2=4x
2,
解得:x=1,或x=-1(舍去),
則半徑OA=2x=2cm.
故答案為:2.
點評:此題考查了垂徑定理,勾股定理,等腰三角形的性質,以及含30°直角三角形的性質,利用了方程的思想,在圓中遇到弦,常常過圓心作弦的垂線,根據垂徑定理由垂直得中點,進而由弦長的一半,圓的半徑及弦心距構造直角三角形,利用勾股定理來解決問題.

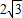 cm,∠AOB=120°,則⊙O的半徑為 cm.
cm,∠AOB=120°,則⊙O的半徑為 cm.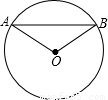

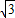 cm,
cm, AB=
AB=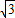 cm,
cm, ∠AOB=60°,
∠AOB=60°,

 標系.
標系.