
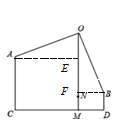
【題目】在一款名為超級瑪麗的游戲中,瑪麗到達一個高為10米的高臺A,利用旗桿頂部的繩索,劃過90°到達與高臺A水平距離為17米,高為3米的矮臺B,

(1)求高臺A比矮臺B高多少米?
(2)求旗桿的高度OM;
(3)瑪麗在蕩繩索過程中離地面的最低點的高度MN.
【答案】(1)7米;(2)OM=15m;(3)瑪麗在蕩繩索過程中離地面的最低點的高度MN為2米.
【解析】試題分析:(1)作差.(2) 作AE⊥OM,BF⊥OM,證明在△AOE和△OBF相似,可以計算出OE+OF長度,最后算出OM長度.(3)利用勾股定理求出半徑長度,作差求MN長度.
試題解析:
(1)10-3=7(米).
(2)作AE⊥OM于E,,BF⊥OM與F,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
 ,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
則2EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m.
(3)由勾股定理得ON=OA=13,
所以MN=15﹣13=2(m).
答:瑪麗在蕩繩索過程中離地面的最低點的高度MN為2米.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】動畫片《喜羊羊與灰太狼》中,“喜羊羊”和“灰太狼”每天都是斗來斗去,每次都是以“灰太狼”的:“我還會回來的!”結束,但有一次,由于“喜羊羊”的疏忽大意,“喜羊羊”被“灰太狼”抓住了,為了讓“喜羊羊”心甘情愿地被他吃掉,“灰太狼”決定把自己苦想多日才解決的問題“已知![]() ,求x-2 0152的值”讓“喜羊羊”在5分鐘之內完成,如果能完成,則放了“喜羊羊”,否則就會被吃掉.“喜羊羊”想了一會,就把問題解決了,“灰太狼”只好把“喜羊羊”放了,那么你知道“喜羊羊”是怎樣做的嗎?請你完成.
,求x-2 0152的值”讓“喜羊羊”在5分鐘之內完成,如果能完成,則放了“喜羊羊”,否則就會被吃掉.“喜羊羊”想了一會,就把問題解決了,“灰太狼”只好把“喜羊羊”放了,那么你知道“喜羊羊”是怎樣做的嗎?請你完成.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分10分)拋物線![]() 與x軸交與
與x軸交與![]() ,
,![]() 兩點,
兩點,

(1)求該拋物線的解析式;
(2)設(1)中的拋物線與y軸交于C點,在該拋物線的對稱軸上是否存在點Q,使得△QAC的周長最小?若存在,求出Q點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年“中國好聲音”全國巡演重慶站在奧體中心舉行.童童從家出發前往觀看,先勻速步行至輕軌車站,等了一會兒,童童搭乘輕軌至奧體中心觀看演出,演出結束后,童童搭乘鄰居劉叔叔的車順利到家.其中x表示童童從家出發后所用時間,y表示童童離家的距離.下圖能反映y與x的函數關系式的大致圖象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩城市為了解決空氣質量污染問題,對城市及其周邊的環境污染進行了綜合治理.在治理過程中,環保部門每月初對兩個城市的空氣質量進行監測,連續10個月的空氣污染指數如下圖所示.其中,空氣污染指≤50時,空氣質量為優;50<空氣污染指數≤100時,空氣質量為良;100<空氣污染指數≤150時,空氣質量為輕微污染.

(1)請填寫下表:
平均數 | 方差 | 中位數 | 空氣質量為優的次數 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)請回答下面問題:
①從平均數和中位數來分析,甲、乙兩個城市的空氣質量;
②從平均數和方差來分析,甲、乙兩個城市的空氣質量變化情況;
③根據折線圖上兩城市的空氣污染指數的走勢及優的情況來分析兩城市治理環境污染的效果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
第1個等式:a1= ![]() =
= ![]() ×(1﹣
×(1﹣ ![]() );
);
第2個等式:a2= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
第3個等式:a3= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
第4個等式:a4= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
…
請解答下列問題:
(1)按以上規律列出第5個等式:a5=;
(2)用含有n的代數式表示第n個等式:an==(n為正整數);
(3)求a1+a2+a3+a4+…+a100的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com