
【題目】甲、乙兩城市為了解決空氣質量污染問題,對城市及其周邊的環境污染進行了綜合治理.在治理過程中,環保部門每月初對兩個城市的空氣質量進行監測,連續10個月的空氣污染指數如下圖所示.其中,空氣污染指≤50時,空氣質量為優;50<空氣污染指數≤100時,空氣質量為良;100<空氣污染指數≤150時,空氣質量為輕微污染.

(1)請填寫下表:
平均數 | 方差 | 中位數 | 空氣質量為優的次數 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)請回答下面問題:
①從平均數和中位數來分析,甲、乙兩個城市的空氣質量;
②從平均數和方差來分析,甲、乙兩個城市的空氣質量變化情況;
③根據折線圖上兩城市的空氣污染指數的走勢及優的情況來分析兩城市治理環境污染的效果.
【答案】(1)填表見解析;(2)乙;甲;乙
【解析】試題分析:(1)根據折線圖,可得甲乙的數據,根據平均數、方差、中位數的計算方法,計算可得表中的數據;
(2)根據(1)的數據,依次比較可得答案,
①平均數相同,比較中位數可得,甲的中位數大于乙的中位數,進而可得答案,
②平均數相同,比較方差可得,甲的方差小于乙的方差,進而可得答案,
③根據折線圖,分析兩地的空氣污染指數的走勢,易得答案.
試題解析:(1)根據折線圖,甲的數據依次為:110、90、100、80、90、60、90、50、70、60,有1次空氣質量為優;乙的數據依次為:120、120、110、110、90、70、60、50、40、30;有3次空氣質量為優;進而可得乙的平均數為:![]() (120+120+110+110+90+70+60+50+40+30)=80,甲的中位數為
(120+120+110+110+90+70+60+50+40+30)=80,甲的中位數為![]() (80+90)=85,填表可得:
(80+90)=85,填表可得:
平均數 | 方差 | 中位數 | 空氣質量為優的次數 | |
甲 | 80 | 340 | 85 | 1 |
乙 | 80 | 1060 | 80 | 3 |


 培優三好生系列答案
培優三好生系列答案科目:初中數學 來源: 題型:
【題目】在一款名為超級瑪麗的游戲中,瑪麗到達一個高為10米的高臺A,利用旗桿頂部的繩索,劃過90°到達與高臺A水平距離為17米,高為3米的矮臺B,

(1)求高臺A比矮臺B高多少米?
(2)求旗桿的高度OM;
(3)瑪麗在蕩繩索過程中離地面的最低點的高度MN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解決問題
平面內的兩條直線相交和平行兩種位置關系,如圖①,若AB∥CD,點P在AB、CD外部,則有∠B=∠BOD,又因為∠BOD是△POD的外角,所以∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.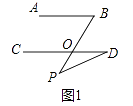
(1)將點P移到AB、CD內部,其余條件不變,如圖②,以上結論是否成立?若成立,說明理由;若不成立,則∠BPD、∠B、∠D之間有何數量關系?請證明你的結論; 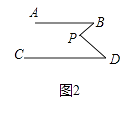
(2)在圖②中,將直線AB繞點B逆時針方向旋轉一定角度交直線CD于點Q,如圖③,能否借助(1)中的圖形與結論,找出圖③中∠BPD、∠B、∠D、∠BQD之間有何數量關系?并說明理由. 
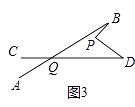
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答
(1)由大小相同的小立方塊搭成的幾何體如圖1,請在圖2的方格中畫出該幾何體的俯視圖和左視圖. 
(2)用小立方體搭一個幾何體,使得它的俯視圖和左視圖與你在方格中所畫的一致,則這樣的幾何體最少要個小立方塊,最多要個小立方塊.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖a,在平面直角坐標系中,A、B坐標分別為(6,0),(0,6),P為線段AB上的一點.
(1) 如圖a,若三角形OAP的面積是12,求點P的坐標;
(2)如圖b,若P為AB的中點,點M,N分別是OA,OB邊上的動點,點M從頂點A,點N從頂點O同時出發,且它們的速度都為1cm/s,則在M,N運動的過程中,線段PM,PN之間有何關系?并證明;
(3)如圖c,若P為線段AB上異于A,B的任意一點,過B點作BD⊥OP,交OP,OA分別于F,D兩點,E為OA上一點,且∠PEA=∠BDO,試判斷線段OD與AE的數量關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com