
【題目】《九章算術》是中國古代的數學專著,是“算經十書”(漢唐之間出現的十部古算書)中最重要的一種.書中有下列問題:“今有邑方不知大小,各中開門,出北門八十步有木,出西門二百四十五步見木,問邑方有幾何?”意思是:如圖,點![]() 、點
、點![]() 分別是正方形
分別是正方形![]() 的邊
的邊![]() 、
、![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() 過點
過點![]() ,
,![]() 步,
步,![]() 步,則正方形的邊長為( )
步,則正方形的邊長為( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】某高科技產品開發公司現有員工50名,所有員工的月工資情況如下表:
員工 | 管理人員 | 普通工作人員 | |||||
人員結構 | 總經理 | 部門經理 | 科研人員 | 銷售人員 | 高級技工 | 中級技工 | 勤雜工 |
員工數(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工資(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
請你根據上述內容,解答下列問題:
(1)該公司“高級技工”有 名;
(2)所有員工月工資的平均數x為2500元,中位數為 元,眾數為 元;
(3)小張到這家公司應聘普通工作人員.請你回答右圖中小張的問題,并指出用(2)中的哪個數據向小張介紹員工的月工資實際水平更合理些;
(4)去掉四個管理人員的工資后,請你計算出其他員工的月平均工資![]() (結果保留整數),并判斷
(結果保留整數),并判斷![]() 能否反映該公司員工的月工資實際水平.
能否反映該公司員工的月工資實際水平.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中是真命題的是( )
A.中位數就是一組數據中最中間的一個數
B.這組數據0,2,3,3,4,6的方差是2.1
C.一組數據的標準差越大,這組數據就越穩定
D.如果![]() 的平均數是
的平均數是![]() ,那么
,那么![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在①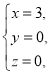 ②
②![]() ③
③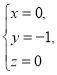 這三對數值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程組
這三對數值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程組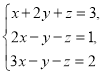 的解.
的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一節數學實踐活動課上,老師拿出三個邊長都為5cm 的正方形硬紙板,他向同學們提出了這樣一個問題:若將三個正方形紙板不重疊地放在桌面上,用一個圓形硬紙板將其蓋住,這樣的圓形硬紙板的最小直徑應有多大?問題提出后,同學們經過討論,大家覺得本題實際上就是求將三個正方形硬紙板無重疊地適當放置,圓形硬紙板能蓋住時的最小直徑.老師將同學們討論過程中探索出的三種不同擺放類型的圖形畫在黑板上,如圖所示:
(1)通過計算(結果保留根號與π).
(Ⅰ)圖①能蓋住三個正方形所需的圓形硬紙板最小直徑應為
(Ⅱ)圖②能蓋住三個正方形所需的圓形硬紙板最小直徑為
(Ⅲ)圖③能蓋住三個正方形所需的圓形硬紙板最小直徑為
(2)其實上面三種放置方法所需的圓形硬紙板的直徑都不是最小的,請你畫出用圓形硬紙板蓋住三個正方形時直徑最小的放置方法,(只要畫出示意圖,不要求說明理由),并求出此時圓形硬紙板的直徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
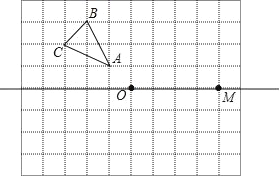
【題目】如圖,它是一個8×10的網格,每個小正方形的邊長均為1,每個小正方形的頂點叫格點,△ABC的頂點均在格點上.
(1)畫出△ABC關于直線OM對稱的△A1B1C1.
(2)畫出△ABC關于點O的中心對稱圖形△A2B2C2.
(3)△A1B1C1與△A2B2C2組成的圖形是軸對稱圖形嗎?如果是,請畫出對稱軸.△A1B1C1與△A2B2C2組成的圖形 (填“是”或“不是”)軸對稱圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,AB∥CD,求∠A+∠AEC+∠C的度數.
解:過點E作EF∥AB.
∵EF∥AB(已作)
∴∠A+∠AEF=180°(______)
又∵AB∥CD(已知)
∴EF∥CD(______)
∴∠CEF+∠______=180°(兩直線平行,同旁內角互補)
∴∠A+∠AEF+∠CEF+∠C=360°(等式性質)
即∠A+∠AEC+∠C=______.
(2)根據上述解題及作輔助線的方法,在圖2中,AB∥EF,則∠B+∠C+∠D+∠E=______.
(3)根據(1)和(2)的規律,圖3中AB∥GF,猜想:∠B+∠C+∠D+∠E+∠F=______.
(4)如圖4,AB∥CD,在B,D兩點的同一側有M1,M2,M3,…Mn共n個折點,則∠B+∠M1+∠M2+…+∠Mn+∠D的度數為______(用含n的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+2ax+c的圖象與x軸交于A、B兩點(點A在點B的左邊)AB=4,與y軸交于點C,OC=OA,點D為拋物線的頂點.
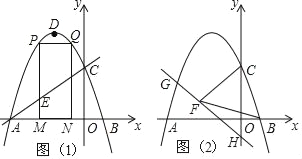
(1)求拋物線的解析式;
(2)點M(m,0)為線段AB上一點(點M不與點A、B重合),過點M作x軸的垂線,與直線AC交于點E,與拋物線交于點P,過點P作PQ∥AB交拋物線于點Q,過點Q作QN⊥x軸于點N,可得矩形PQNM,如圖1,點P在點Q左邊,當矩形PQNM的周長最大時,求m的值,并求出此時的△AEM的面積;
(3)已知H(0,﹣1),點G在拋物線上,連HG,直線HG⊥CF,垂足為F,若BF=BC,求點G的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了了解學生每天完成家庭作業所用時間的情況,從每班抽取相同數量的學生進行調查,并將所得數據進行整理,制成條形統計圖和扇形統計圖,如圖所示:


(1)補全條形統計圖;
(2)求扇形統計圖中扇形D的圓心角的度數;
(3)若該中學有2000名學生,請估計其中有多少名學生能在1.5 h內完成家庭作業.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com