【題目】如圖，已知點
，點
是直線上的兩點，
厘米，點
在線段
上，且
厘米，點
、點
是直線上的兩個動點，點的速度為1厘米/秒，點的速度為2厘米/秒，點
分別從點、點同時出發在直線上運動，則經過多少秒時線段
的長為5厘米.
科目：初中數學 來源： 題型：
【題目】（類比學習）規定：求若干個相同的有理數（均不等于0）的除法運算叫做除方，如4÷4÷4，（-2）÷（-2）÷（-2）÷（-2）÷（-2）等.類比有理數的乘方，我們把4÷4÷4記作
，讀作“4的3次除方”，（-2）÷（-2）÷（-2）÷（-2）÷（-2）記作
，讀作“-2的5次除方”.
（探究活動）（1）直接寫出計算結果：
= ；
（2）下列說法不正確的是（ ）
A．任何非零有理數的2次除方都等于1 B．負數的奇數次除方是負數
C．負數的偶數次除方是正數 D．3的2次除方等于2的3次除方
（深入思考）有理數的乘方運算可以轉化為乘法運算，從而得出結果.那么有理數的除方運算與熟悉的運算一起，該如何進行？有理數的除方與有理數的乘方之間有何聯系？
（3）計算：
（4）直接寫出2019與
之間的關系：
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某班要在一面墻上同時展示數張形狀、大小均相同的矩形繪畫作品，將這些作品排成一個矩形（作品不完全重合）．現需要在每張作品的四個角落都釘上圖釘，如果作品有角落相鄰，那么相鄰的角落共享一枚圖釘（例如用9枚圖釘將4張作品釘在墻上如圖）．若有28枚圖釘可供選用，則最多可以展示繪畫作品（ ）
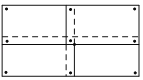
A. 16張B. 18張C. 20張D. 21張
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知A，B兩地相距120千米，甲乙兩人沿同一條公路勻速行駛，甲騎自行車以20千米/時從A地前往B地，同時乙騎摩托車從B地前往A地，設兩人之間的距離為s（千米），甲行駛的時間為t（小時），若s與t的函數關系如圖所示，則下列說法錯誤的是（ ）
A.經過2小時兩人相遇
B.若乙行駛的路程是甲的2倍，則t=3
C.當乙到達終點時，甲離終點還有60千米
D.若兩人相距90千米，則t=0.5或t=4.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：
數軸上線段的長度可以用線段端點表示的數進行減法運算得到，例如圖，線段AB＝1＝0﹣（﹣1）；線段 BC＝2＝2﹣0；線段 AC＝3＝2﹣（﹣1）問題
①數軸上點M、N代表的數分別為﹣9和1，則線段MN＝ ；
②數軸上點E、F代表的數分別為﹣6和﹣3，則線段EF＝ ；
③數軸上的兩個點之間的距離為5，其中一個點表示的數為2，則另一個點表示的數為m，求m．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場第一次用11000元購進某款拼裝機器人進行銷售，很快銷售一空，商家又用24000元第二次購進同款機器人，所購進數量是第一次的2倍，但單價貴了10元．
（1）求該商家第一次購進機器人多少個？
（2）若所有機器人都按相同的標價銷售，要求全部銷售完畢的利潤率不低于20%（不考慮其它因素），那么每個機器人的標價至少是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，O為菱形ABCD的對稱中心，已知C（2，0），D（0，﹣1），N為線段CD上一點（不與C、D重合）．
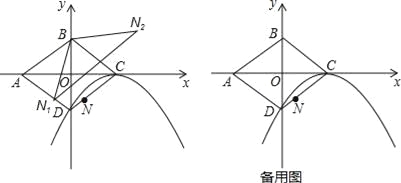
（1）求以C為頂點，且經過點D的拋物線解析式；
（2）設N關于BD的對稱點為N1，N關于BC的對稱點為N2，求證：△N1BN2∽△ABC；
（3）求（2）中N1N2的最小值；
（4）過點N作y軸的平行線交（1）中的拋物線于點P，點Q為直線AB上的一個動點，且∠PQA=∠BAC，求當PQ最小時點Q坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司計劃購買A、B兩種計算器共100個，要求A種計算器數量不低于B種的
，且不高于B種的
．已知A、B兩種計算器的單價分別是150元/個、100元/個，設購買A種計算器x個．
（1）求計劃購買這兩種計算器所需費用y（元）與x的函數關系式；
（2）問該公司按計劃購買者兩種計算器有多少種方案？
（3）由于市場行情波動，實際購買時，A種計算器單價下調了3m（m＞0）元/個，同時B種計算器單價上調了2m元/個，此時購買這兩種計算器所需最少費用為12150元，求m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
