
【題目】在平面直角坐標(biāo)系中,點(diǎn)![]() 是原點(diǎn),四邊形
是原點(diǎn),四邊形![]() 是矩形,點(diǎn)
是矩形,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() .以點(diǎn)
.以點(diǎn)![]() 為中心,順時(shí)針旋轉(zhuǎn)矩形
為中心,順時(shí)針旋轉(zhuǎn)矩形![]() ,得到矩形
,得到矩形![]() ,點(diǎn)
,點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)分別為
的對(duì)應(yīng)點(diǎn)分別為![]() .
.
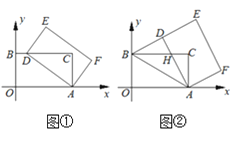
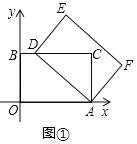
(1)如圖①,當(dāng)點(diǎn)![]() 落在
落在![]() 邊上時(shí),求點(diǎn)
邊上時(shí),求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
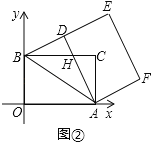
(2)如圖②,當(dāng)點(diǎn)![]() 落在線(xiàn)段
落在線(xiàn)段![]() 上時(shí),
上時(shí),![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() .求點(diǎn)
.求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)記![]() 為矩形
為矩形![]() 對(duì)角線(xiàn)的交點(diǎn),
對(duì)角線(xiàn)的交點(diǎn),![]() 為
為![]() 的面積,求
的面積,求![]() 的取值范圍(直接寫(xiě)出結(jié)果即可).
的取值范圍(直接寫(xiě)出結(jié)果即可).
【答案】(1)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ;(2)點(diǎn)
;(2)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ;(3)
;(3)![]() .
.
【解析】
(1)如圖①,在Rt△ACD中求出CD即可解決問(wèn)題;
(2)設(shè)AH=BH=m,則HC=BC-BH=5-m,在Rt△AHC中,根據(jù)AH2=HC2+AC2,構(gòu)建方程求出m即可解決問(wèn)題;
(3)如圖③中,當(dāng)點(diǎn)D在線(xiàn)段BK上時(shí),△DEK的面積最小,當(dāng)點(diǎn)D在BA的延長(zhǎng)線(xiàn)上時(shí),△D′E′K的面積最大,求出面積的最小值以及最大值即可解決問(wèn)題;
解:(1)如圖①中,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四邊形
四邊形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,![]() ,
,
![]() 矩形
矩形![]() 是由矩形
是由矩形![]() 旋轉(zhuǎn)得到,
旋轉(zhuǎn)得到,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
(2)如圖②中,
由四邊形![]() 是矩形,得到
是矩形,得到![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 在線(xiàn)段
在線(xiàn)段![]() 上,
上,
∴![]() ,
,
由(1)可知,![]() ,又
,又![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,
又在矩形![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
(3)如圖③中,當(dāng)點(diǎn)![]() 在線(xiàn)段
在線(xiàn)段![]() 上時(shí),
上時(shí),![]() 的面積最小,最小值
的面積最小,最小值![]() ,
,
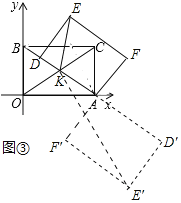
當(dāng)點(diǎn)![]() 在
在![]() 的延長(zhǎng)線(xiàn)上時(shí),△
的延長(zhǎng)線(xiàn)上時(shí),△![]() 的面積最大,最大面積
的面積最大,最大面積![]() .
.
綜上所述,![]() .
.


 黃岡小狀元解決問(wèn)題天天練系列答案
黃岡小狀元解決問(wèn)題天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司根據(jù)市場(chǎng)需求銷(xiāo)售A、B兩種型號(hào)的凈水器,每臺(tái)A型凈水器比每臺(tái)B型凈水器進(jìn)價(jià)多200元,用5萬(wàn)元購(gòu)進(jìn)A型凈水器與用4.5萬(wàn)元購(gòu)進(jìn)B型凈水器的數(shù)量相等.
(1)求每臺(tái)A型、B型凈水器的進(jìn)價(jià)各是多少元?
(2)該公司計(jì)劃用不超過(guò)9.8萬(wàn)元購(gòu)進(jìn)A,B兩種型號(hào)的凈水器共50臺(tái),其中A型、B型凈水器每臺(tái)售價(jià)分別為2500元、2180元,設(shè)A型凈水器為x臺(tái).
①求x的取值范圍.
②若公司決定從銷(xiāo)售A型凈水器的利潤(rùn)中每臺(tái)捐獻(xiàn)a(100<a<150)元給貧困村飲水改造愛(ài)心工程,求售完這50臺(tái)凈水器后獲得的最大利潤(rùn).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2016年,某貧困戶(hù)的家庭年人均純收入為2500元,通過(guò)政府產(chǎn)業(yè)扶持,發(fā)展了養(yǎng)殖業(yè)后,到2018年,家庭年人均純收入達(dá)到了3600元.
(1)求該貧困戶(hù)2016年到2018年家庭年人均純收入的年平均增長(zhǎng)率;
(2)若年平均增長(zhǎng)率保持不變,2019年該貧困戶(hù)的家庭年人均純收入是否能達(dá)到4200元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】校園內(nèi)有一個(gè)由兩個(gè)全等的六邊形(邊長(zhǎng)為![]() )圍成的花壇,現(xiàn)將這個(gè)花壇在原有的基礎(chǔ)上擴(kuò)建成如圖所示的一個(gè)菱形區(qū)域,并在新擴(kuò)建的部分種上草坪,則擴(kuò)建后菱形區(qū)域的周長(zhǎng)為( )
)圍成的花壇,現(xiàn)將這個(gè)花壇在原有的基礎(chǔ)上擴(kuò)建成如圖所示的一個(gè)菱形區(qū)域,并在新擴(kuò)建的部分種上草坪,則擴(kuò)建后菱形區(qū)域的周長(zhǎng)為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,小明的家在某住宅樓AB的最頂層(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道這座建筑物的高度,于是在自家陽(yáng)臺(tái)的A處測(cè)得建筑物CD的底部C的俯角是43°,頂部D的仰角是25°,他又測(cè)得兩建筑物之間的距離BC是28米,請(qǐng)你幫助小明求出建筑物CD的高度(精確到1米).
(參考數(shù)據(jù):sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
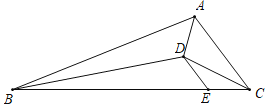
【題目】在△ABC中,AC=6,AB=14,BC=16,點(diǎn)D是△ABC的內(nèi)心,過(guò)D作DE∥AC交BC于E,則DE的長(zhǎng)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
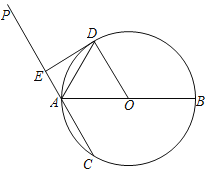
【題目】如圖,AB是⊙O的直徑,過(guò)點(diǎn)A的直線(xiàn)PC交⊙O于A,C兩點(diǎn),AD平分∠PAB,射線(xiàn)AD交⊙O于點(diǎn)D,過(guò)點(diǎn)D作DE⊥PA于點(diǎn)E.
(1)求證:ED為⊙O的切線(xiàn);
(2)若AB=10,ED=2AE,求AC的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
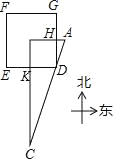
【題目】《九章算術(shù)》是中國(guó)傳統(tǒng)數(shù)學(xué)最重要的著作,在“勾股”章中有這樣一個(gè)問(wèn)題:“今有邑方二百步,各中開(kāi)門(mén),出東門(mén)十五步有木,問(wèn):出南門(mén)幾步面見(jiàn)木?”用今天的話(huà)說(shuō),大意是:如圖,DEFG是一座邊長(zhǎng)為200步(“步”是古代的長(zhǎng)度單位)的正方形小城,東門(mén)H位于GD的中點(diǎn),南門(mén)K位于ED的中點(diǎn),出東門(mén)15步的A處有一樹(shù)木,求出南門(mén)多少步恰好看到位于A處的樹(shù)木(即點(diǎn)D在直線(xiàn)AC上)?請(qǐng)你計(jì)算KC的長(zhǎng)為多少步.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
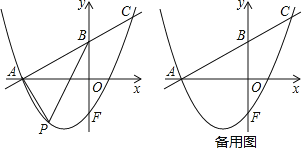
【題目】如圖,已知在平面直角坐標(biāo)系xOy中,直線(xiàn)y=![]() x+
x+![]() 與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,點(diǎn)F是點(diǎn)B關(guān)于x軸的對(duì)稱(chēng)點(diǎn),拋物線(xiàn)y=
與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,點(diǎn)F是點(diǎn)B關(guān)于x軸的對(duì)稱(chēng)點(diǎn),拋物線(xiàn)y=![]() x2+bx+c經(jīng)過(guò)點(diǎn)A和點(diǎn)F,與直線(xiàn)AB交于點(diǎn)C.
x2+bx+c經(jīng)過(guò)點(diǎn)A和點(diǎn)F,與直線(xiàn)AB交于點(diǎn)C.
(1)求b和c的值;
(2)點(diǎn)P是直線(xiàn)AC下方的拋物線(xiàn)上的一動(dòng)點(diǎn),連結(jié)PA,PB.求△PAB的最大面積及點(diǎn)P到直線(xiàn)AC的最大距離;
(3)點(diǎn)Q是拋物線(xiàn)上一點(diǎn),點(diǎn)D在坐標(biāo)軸上,在(2)的條件下,是否存在以A,P,D,Q為頂點(diǎn)且AP為邊的平行四邊形,若存在,直接寫(xiě)出點(diǎn)Q的坐標(biāo);若不存在,說(shuō)明理由.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com