
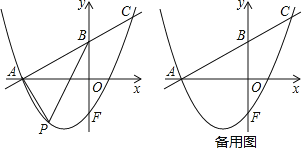
【題目】如圖,已知在平面直角坐標系xOy中,直線y=![]() x+
x+![]() 與x軸交于點A,與y軸交于點B,點F是點B關于x軸的對稱點,拋物線y=
與x軸交于點A,與y軸交于點B,點F是點B關于x軸的對稱點,拋物線y=![]() x2+bx+c經過點A和點F,與直線AB交于點C.
x2+bx+c經過點A和點F,與直線AB交于點C.
(1)求b和c的值;
(2)點P是直線AC下方的拋物線上的一動點,連結PA,PB.求△PAB的最大面積及點P到直線AC的最大距離;
(3)點Q是拋物線上一點,點D在坐標軸上,在(2)的條件下,是否存在以A,P,D,Q為頂點且AP為邊的平行四邊形,若存在,直接寫出點Q的坐標;若不存在,說明理由.
【答案】(1)b=![]() ,c=﹣
,c=﹣![]() ;(2)
;(2)![]() ,
,![]() ;(3)點Q的坐標為:(﹣1﹣
;(3)點Q的坐標為:(﹣1﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,則點
,則點![]() 、
、![]() 的坐標分別為:
的坐標分別為:![]() 、
、![]() ,則點
,則點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() 和點
和點![]() ,則
,則![]() ,將點
,將點![]() 的坐標代入拋物線表達式并解得:
的坐標代入拋物線表達式并解得:![]() ;
;
(2)過點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,設出點P,H的坐標,將△PAB的面積表示成△APH和△BPH的面積之和,可得函數表達式,可求△PAB的面積最大值,此時設點P到AB的距離為d,當△PAB的面積最大值時d最大,利用面積公式求出d.
,設出點P,H的坐標,將△PAB的面積表示成△APH和△BPH的面積之和,可得函數表達式,可求△PAB的面積最大值,此時設點P到AB的距離為d,當△PAB的面積最大值時d最大,利用面積公式求出d.
(3)若存在以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點且
為頂點且![]() 為邊的平行四邊形時,平移AP,得出所有可能的情形,利用平行四邊形的對稱性得到坐標的關系,即可求解.
為邊的平行四邊形時,平移AP,得出所有可能的情形,利用平行四邊形的對稱性得到坐標的關系,即可求解.
解:(1)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
令x=0,則y=![]() ,令y=0,則x=-3,
,令y=0,則x=-3,
則點![]() 、
、![]() 的坐標分別為:
的坐標分別為:![]() 、
、![]() ,
,
∵點F是點B關于x軸的對稱點,
∴點![]() ,
,
∵拋物線![]() 經過點
經過點![]() 和點
和點![]() ,則
,則![]() ,
,
將點![]()
![]() 代入拋物線表達式得:
代入拋物線表達式得:![]() ,
,
解得:![]() ,
,
故拋物線的表達式為:![]() ,
,
![]() ,
,![]() ;
;
(2)過點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,
,
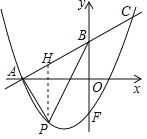
設點![]() ,則點
,則點![]() ,
,
則![]() 的面積:
的面積:
![]()
![]()
當![]() 時,
時,
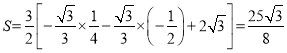 ,
,
且![]() ,
,
∴![]() 的最大值為
的最大值為![]() ,此時點
,此時點![]() ,
,![]() ,
,
設:![]() 到直線
到直線![]() 的最大距離為
的最大距離為![]() ,
,![]()
![]() ,解得:
,解得:![]() ;
;
(3)存在,理由:
點![]() ,點
,點![]() ,
,![]() ,設點
,設點![]() ,
,![]() ,
,
①當點![]() 在
在![]() 軸上時,
軸上時,
若存在以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點且
為頂點且![]() 為邊的平行四邊形時,如圖,
為邊的平行四邊形時,如圖,
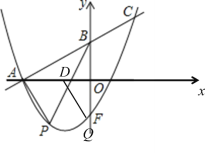
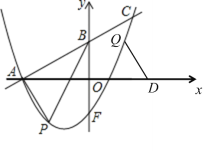
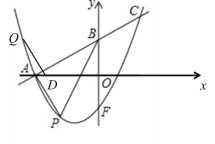
三種情形都可以構成平行四邊形,
由于平行四邊形的對稱性可得圖中點Q到x軸的距離和點P到x軸的距離相等,
∴![]() ,
,
即![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() 或
或![]() ;
;
②當點![]() 在
在![]() 軸上時,如圖:
軸上時,如圖:
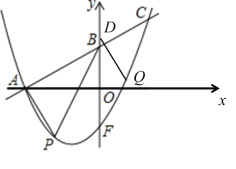
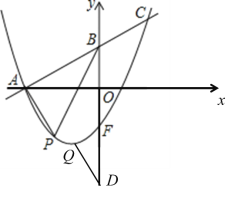
當點Q在y軸右側時,由平行四邊形的性質可得:
![]() =3,
=3,
∴![]()
∴m=![]() ,代入二次函數表達式得:y=
,代入二次函數表達式得:y=![]()
當點Q在y軸左側時,由平行四邊形的性質可得:
![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,代入二次函數表達式得:y=
,代入二次函數表達式得:y=![]()
故點![]() ,
,![]() 或
或![]() ,
,![]() ;
;
故點![]() 的坐標為:
的坐標為:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
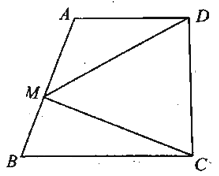
【題目】如圖,在直角梯形 ABCD 中,AD / /BC ,AD CD ,M 為腰 AB 上一動點,聯結 MC 、MD , AD 10, BC 15 , cot B ![]() ,求:
,求:
(1)線段CD 的長.
(2)設線段 BM 的長為 x ,△CDM的面積為 y ,求 y 關于 x 的函數解析式,并寫出它的定義域.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應“學雷鋒、樹新風、做文明中學生”的號召,某校開展了志愿者服務活動,活動項目有“防疫宜宣傳”、“文明交通崗”、“關愛老人”、“義務植樹”、“社區服務”五項,活動期間,隨機抽取了部分學生對志思者服務情況進行調查,結果發現,被調查的每名學生都參與了活動,最少的參與了1項,最多的參與了5項,根據調查結果繪制了如下不完整的條形統計圖和扇形統計圖.
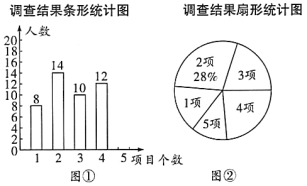
根據以上統計圖解答下列問題:
(1)本次隨機抽取的學生共有______名;
(2)補全條形統計圖;
(3)若該校有3000名學生,請估計參與了4項活動的學生人數;
(4)在所調查的學生中隨機選取一人談活動心得,求選中參與了5項活動的學生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠為貫徹落實“綠水青山就是金山銀山“的發展理念,投資組建了日廢水處理量為m噸的廢水處理車間,對該廠工業廢水進行無害化處理. 但隨著工廠生產規模的擴大,該車間經常無法完成當天工業廢水的處理任務,需要將超出日廢水處理量的廢水交給第三方企業處理. 已知該車間處理廢水,每天需固定成本30元,并且每處理一噸廢水還需其他費用8元;將廢水交給第三方企業處理,每噸需支付12元.根據記錄,5月21日,該廠產生工業廢水35噸,共花費廢水處理費370元.
(1)求該車間的日廢水處理量m;
(2)為實現可持續發展,走綠色發展之路,工廠合理控制了生產規模,使得每天廢水處理的平均費用不超過10元/噸,試計算該廠一天產生的工業廢水量的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
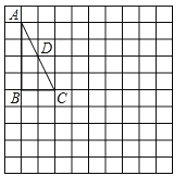
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 為邊
為邊![]() 的中點,請按下列要求作圖,并解決問題:
的中點,請按下列要求作圖,并解決問題:
(1)作點![]() 關于
關于![]() 的對稱點
的對稱點![]() ;
;
(2)在(1)的條件下,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,
,
①面出旋轉后的![]() (其中
(其中![]() 、
、![]() 、
、![]() 三點旋轉后的對應點分別是點
三點旋轉后的對應點分別是點![]() 、
、![]() 、
、![]() );
);
②若![]() ,則
,則![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校分別有一男一女共4名教師報名到農村中學支教.
(1)若從甲、乙兩校報名的教師中分別隨機選1名,則所選的2名教師性別相同的概率是 .
(2)若從報名的4名教師中隨機選2名,用列表或畫樹狀圖的方法求出這2名教師來自同一所學校的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若干個全等的正五邊形排成環狀,圖中所示的是前3個正五邊形,要完成這一圓環還需正五邊形的個數為( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com