
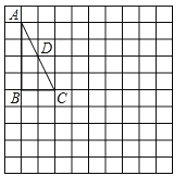
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 為邊
為邊![]() 的中點,請按下列要求作圖,并解決問題:
的中點,請按下列要求作圖,并解決問題:
(1)作點![]() 關于
關于![]() 的對稱點
的對稱點![]() ;
;
(2)在(1)的條件下,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,
,
①面出旋轉后的![]() (其中
(其中![]() 、
、![]() 、
、![]() 三點旋轉后的對應點分別是點
三點旋轉后的對應點分別是點![]() 、
、![]() 、
、![]() );
);
②若![]() ,則
,則![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)
【答案】(1)見解析;(2)①見解析,②90°α
【解析】
(1)利用網格特點和軸對稱的性質畫出O點;
(2)①利用網格特點和旋轉的性質分別畫出A、B、C三點對應點點E、F、G即可;
②先確定∠OCB=∠DCB=α,再利用OB=OC和三角形內角和得到∠BOC=180°2α,根據旋轉的性質得到∠COG=90°,則∠BOG=270°2α,于是可計算出∠OGB=α45°,然后計算∠OGC∠OGB即可.
(1)如圖,點O為所作;
(2)①如圖,△EFG為所作;
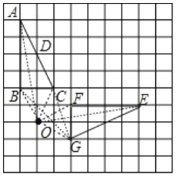
②∵點O與點D關于BC對稱,
∴∠OCB=∠DCB=α,
∵OB=OC,
∴∠OBC=∠OCB=α,
∴∠BOC=180°2α,
∵∠COG=90°,
∴∠BOG=180°2α+90°=270°2α,
∵OB=OG,
∴∠OGB=![]() [180°(270°2α)]=α45°,
[180°(270°2α)]=α45°,
∴∠BGC=∠OGC∠OGB=45°(α45°)=90°α.
故答案為90°α.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在△ABC 與△DEF 中,下列四個命題是真命題的個數共有( )
①如果A D, ![]() ,那么△ABC 與△DEF相似;
,那么△ABC 與△DEF相似;
②如果A D,![]() ,那么△ABC 與△DEF相似;
,那么△ABC 與△DEF相似;
③如果A D 90°,![]() ,那么△ABC 與△DEF相似;
,那么△ABC 與△DEF相似;
④如果A D 90°, ![]() ,那么△ABC 與△DEF相似.
,那么△ABC 與△DEF相似.
A.1 個B.2 個C.3 個D.4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某球室有三種品牌的![]() 個乒乓球,價格是7,8,9(單位:元)三種.從中隨機拿出一個球,已知
個乒乓球,價格是7,8,9(單位:元)三種.從中隨機拿出一個球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求這![]() 個球價格的眾數;
個球價格的眾數;
(2)若甲組已拿走一個![]() 元球訓練,乙組準備從剩余
元球訓練,乙組準備從剩余![]() 個球中隨機拿一個訓練.
個球中隨機拿一個訓練.
①所剩的![]() 個球價格的中位數與原來
個球價格的中位數與原來![]() 個球價格的中位數是否相同?并簡要說明理由;
個球價格的中位數是否相同?并簡要說明理由;
②乙組先隨機拿出一個球后放回,之后又隨機拿一個,用列表法(如圖)求乙組兩次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目:初中數學 來源: 題型:
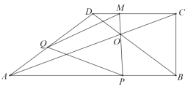
【題目】已知:如圖,四邊形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 開始沿
開始沿![]() 邊勻速運動,運動速度為
邊勻速運動,運動速度為![]() ,動點
,動點![]() 從點
從點![]() 開始沿
開始沿![]() 邊勻速運動,運動速度為
邊勻速運動,運動速度為![]() .點
.點![]() 和點
和點![]() 同時出發,
同時出發,![]() 為四邊形
為四邊形![]() 的對角線的交點,連接
的對角線的交點,連接![]() 并延長交
并延長交![]() 于
于![]() ,連接
,連接![]() .設運動的時間為
.設運動的時間為![]() ,
,![]() .
.
(1)當![]() 為何值時,
為何值時,![]() ?
?
(2)設五邊形![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)在運動過程中,是否存在某一時刻![]() ,使
,使![]() 的面積等于五邊形
的面積等于五邊形![]() 面積的
面積的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(4)在運動過程中,是否存在某一時刻![]() ,使點
,使點![]() 在
在![]() 的垂直平分線上?若存在,求出
的垂直平分線上?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
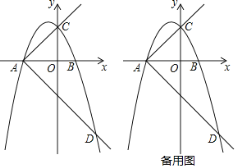
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于點A(﹣2,0)和B(l,0),與y軸交于點C.
(1)求拋物線的表達式;
(2)作射線AC,將射線AC繞點A順時針旋轉90°交拋物線于另一點D,在射線AD上是否存在一點H,使△CHB的周長最小.若存在,求出點H的坐標;若不存在,請說明理由;
(3)在(2)的條件下,點Q為拋物線的頂點,點P為射線AD上的一個動點,且點P的橫坐標為t,過點P作x軸的垂線l,垂足為E,點P從點A出發沿AD方向運動,直線l隨之運動,當﹣2<t<1時,直線l將四邊形ABCQ分割成左右兩部分,設在直線l左側部分的面積為S,求S關于t的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
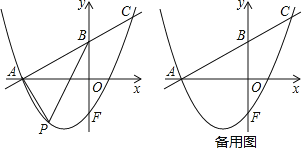
【題目】如圖,已知在平面直角坐標系xOy中,直線y=![]() x+
x+![]() 與x軸交于點A,與y軸交于點B,點F是點B關于x軸的對稱點,拋物線y=
與x軸交于點A,與y軸交于點B,點F是點B關于x軸的對稱點,拋物線y=![]() x2+bx+c經過點A和點F,與直線AB交于點C.
x2+bx+c經過點A和點F,與直線AB交于點C.
(1)求b和c的值;
(2)點P是直線AC下方的拋物線上的一動點,連結PA,PB.求△PAB的最大面積及點P到直線AC的最大距離;
(3)點Q是拋物線上一點,點D在坐標軸上,在(2)的條件下,是否存在以A,P,D,Q為頂點且AP為邊的平行四邊形,若存在,直接寫出點Q的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
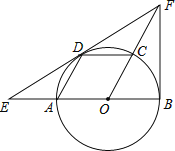
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,且四邊形
上,且四邊形![]() 是平行四邊形,過點
是平行四邊形,過點![]() 作
作![]() 的切線,分別交
的切線,分別交![]() 的延長線與
的延長線與![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() 。
。
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() 的半徑為1,求
的半徑為1,求![]() 的長。
的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一水果店主分兩批購進同一種水果,第一批所用資金為2400元,因天氣原因,水果漲價,第二批所用資金是2700元,但由于第二批單價比第一批單價每箱多10元,以致購買的數量比第一批少25%.
(1)該水果店主購進第一批這種水果每箱的單價是多少元?
(2)該水果店主計劃兩批水果的售價均定為每千克4元,每箱10千克,實際銷售時按計劃無損耗售完第一批后,發現第二批水果品質不如第一批,于是該店主將售價下降a%銷售,結果還是出現了2%的損耗,但這兩批水果銷售完后仍賺了不低于2346元,求a的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,且拋物線與
,且拋物線與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,其中
點,其中![]() ,
,![]() .
.

(1)若直線![]() 經過
經過![]() 、
、![]() 兩點,求直線
兩點,求直線![]() 和拋物線的解析式;
和拋物線的解析式;
(2)在拋物線的對稱軸![]() 上找一點
上找一點![]() ,使點
,使點![]() 到點
到點![]() 的距離與到點
的距離與到點![]() 的距離之和最小,求出點
的距離之和最小,求出點![]() 的坐標;
的坐標;
(3)設點![]() 為拋物線的對稱軸
為拋物線的對稱軸![]() 上的一個動點,求使
上的一個動點,求使![]() 為直角三角形的點
為直角三角形的點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com