
【題目】如圖1,點G是正方形ABCD對角線CA的延長線上任意一點,以線段AG為邊作一個正方形AEFG,線段EB和GD相交于點H.

(1)求證:EB=GD且EB⊥GD;
(2)若AB=2,AG=![]() ,求
,求![]() 的長;
的長;
(3)如圖2,正方形AEFG繞點A逆時針旋轉![]() 連結DE,BG,
連結DE,BG,![]() 與
與![]() 的面積之差是否會發生變化?若不變,請求出
的面積之差是否會發生變化?若不變,請求出![]() 與
與![]() 的面積之差;若變化,請說明理由.
的面積之差;若變化,請說明理由.
【答案】(1)見解析; (2) ![]() ;(3)不變,
;(3)不變,![]() 與
與![]() 的面積之差為0
的面積之差為0
【解析】
(1)在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,得到∠GAD=∠EAB,從而△EAB≌△GAD,即EB=GD;由∠AEB=∠AGD,∠EOH=∠AOG,即可得出∠EHG=∠EAG=90°;
(2)設BD與AC交于點O,由AB=AD=2,在Rt△ABD中求得DB,在Rt△GOD中利用勾股定理即可求得結果;
(3)作BQ⊥GA交GA的延長線于Q,作DP⊥EA交EA于P,可證得∠1=∠2,根據“AAS”可判斷△PDA≌△QBA,所以PD=BQ,然后根據三角形面積公式得到![]() ,保持不變.
,保持不變.
(1)如圖1,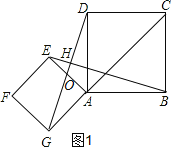
∵四邊形EFGA和四邊形ABCD是正方形,
∴AG=AE,AB=AD,∠EAG=90°,∠DAB=90°,
∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
在△EAB和△GAD中,
 ,
,
∴△EAB≌△GAD(SAS),
∴EB=GD;∠AEB=∠AGD,
∵∠EOH=∠AOG,
∴∠EHG=∠EAG=90°,
∴EB=GD且EB⊥GD;
(2)如圖2,連接BD,BD與AC交于點O,
∵AB=AD=2,
在Rt△ABD中,![]() ,
,
∴AO=DO=![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)不變,![]() .理由如下:
.理由如下:
作BQ⊥GA交GA的延長線于Q,作DP⊥EA交EA于P,如圖3,
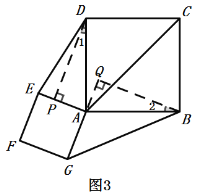
正方形ABCD和正方形AEFG中,
∠EAG=∠DAB=90°,AD=AB,
∴∠EAD+∠BAG+∠EAG+∠DAB =360![]() ,則∠BAG=180°-∠EAD,
,則∠BAG=180°-∠EAD,
∵∠1=90°-∠EAD,∠2=∠BAG -90°=180°-∠EAD -90°=90°-∠EAD,
∴∠1=∠2,
在△PDA和△QBA中,
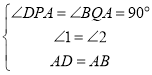 ,
,
∴△PDA≌△QBA(AAS),
∴DP=BQ,
∵![]() ,
,![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題:大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,但是由于1<
的小數部分我們不可能全部地寫出來,但是由于1<![]() <2,所以
<2,所以![]() 的整數部分為1,將
的整數部分為1,將![]() 減去其整數部分1,差就是小數部分
減去其整數部分1,差就是小數部分![]() ,根據以上的內容,解答下面的問題:
,根據以上的內容,解答下面的問題:
(1)![]() 的整數部分是______,小數部分是______;
的整數部分是______,小數部分是______;
(2)![]() 的整數部分是______,小數部分是_____;
的整數部分是______,小數部分是_____;
(3)若設![]() 整數部分是x,小數部分是y,求x﹣
整數部分是x,小數部分是y,求x﹣![]() y的值.
y的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個裝有進水管和出水管的容器,根據實際需要,從某時刻開始的2分鐘內只進水不出水,在隨后的4分鐘內既進水又出水,接著關閉進水管直到容器內的水放完.假設每分鐘的進水量和出水量是兩個常數,容器內的水量y(單位:升)與時間x(單位:分鐘)之間的部分關系如圖所示.
(1)當2≤x≤6時,求y與x的表達式;
(2)請將圖象補充完整;
(3)從進水管開始進水起,求該容器內的水量不少于7.5升所持續時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提高學生的身體素質,并爭取在學校的體育節中獲得好成績,班級準備從體育用品商店購買跳繩和毽子.已知購買5個毽子和3根跳繩共需85元,購買4個毽子和5根跳繩共需120元.
(1)求一個毽子和一根跳繩各需多少元?
(2)由于購買量大,商店給出如下優惠:毽子6個一盒,整盒出售,每盒27元,跳繩八折優惠.已知班級需要購買的毽子數比跳繩數的2倍多10,總費用不超過395元.問班級最多能購買多少根跳繩?
查看答案和解析>>
科目:初中數學 來源: 題型:
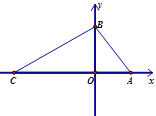
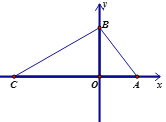
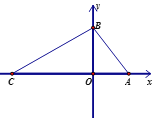
【題目】如圖,在平面直角坐標系中,O為坐標原點,A(a,0),B(0,b),且a,b滿足![]() ,連接AB,AB=5.C(-7,0)是x軸負半軸上一點,連接BC.
,連接AB,AB=5.C(-7,0)是x軸負半軸上一點,連接BC.
(1)求OA、OB的長;
(2)動點P從點B出發,沿BA以每秒2個單位的速度向終點A勻速運動,連接CP,設點P的運動時間為t,△CBP的面積為S,用含t的代數式表示S(不要求寫出t的取值范圍)
(3)在(2)的條件下,連接OP,是否存在t值,使S△BCP=![]() S△PCO,如果存在,求出相應的t值,并直接寫出P點坐標.若不存在,說明理由.
S△PCO,如果存在,求出相應的t值,并直接寫出P點坐標.若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小剛進行賽跑訓練,他們選擇了一個土坡,按同一路線同時出發,從坡腳跑到坡頂再原路返回坡腳.他們倆上坡的平均速度不同,下坡的平均速度則是各自上坡平均速度的1. 5倍.設兩人出發x min后距出發點的距離為y m.圖中折線段OBA表示小明在整個訓練中y與x的函數關系,其中點A在x軸上,點B坐標為(2,480).
(1)點B所表示的實際意義是 ;
(2)求出AB所在直線的函數關系式;
(3)如果小剛上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數![]() 都可以進行這樣的分解:
都可以進行這樣的分解:![]() (
(![]() 是正整數,且
是正整數,且![]() ),在
),在![]() 的所有這種分解中,如果
的所有這種分解中,如果![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是
是![]() 的最佳分解,并規定
的最佳分解,并規定![]() .
.
例如:18可以分解成![]() ,
,![]() ,
,![]() ,因為
,因為![]() ,所以
,所以![]() 是18的最佳分解,所以
是18的最佳分解,所以![]() .
.
(1)如果一個正整數![]() 是另外一個正整數
是另外一個正整數![]() 的平方,我們稱正整數
的平方,我們稱正整數![]() 是完全平方數.
是完全平方數.
求證:對任意一個完全平方數![]() ,總有
,總有![]() ;
;
(2)如果一個兩位正整數![]() ,
,![]() (
(![]() ,
,![]() 為自然數),交換其個位上的數與十位上的數,得到的新數減去原來的兩位正整數所得的差為9,那么我們稱這個
為自然數),交換其個位上的數與十位上的數,得到的新數減去原來的兩位正整數所得的差為9,那么我們稱這個![]() 為“求真抱樸數”,求所有的“求真抱樸數”;
為“求真抱樸數”,求所有的“求真抱樸數”;
(3)在(2)所得的“求真抱樸數”中,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com