
【題目】已知y是x的二次函數,當x=2時,y=﹣4,當y=4時,x恰為方程2x2﹣x﹣8=0的根.
(1)解方程 2x2﹣x﹣8=0
(2)求這個二次函數的解析式.
【答案】
(1)解:∵2x2﹣x﹣8=0,
∴a=2,b=﹣1c=﹣8,
∴△=1+64=65>0,
∴x1= ![]() ,x2=
,x2= ![]()
(2)解:設方程2x2﹣x﹣8=0的根為x1、x2,則
當x=x1,x=x2時,y=4,可設y=a(2x2﹣x﹣8)+4,
把x=2,y=﹣4代入,得﹣4=a(2×22﹣2﹣8)+4,
解得a=4,
所求函數為y=4(2x2﹣x﹣8)+4,
即y=8x2﹣4x﹣28
【解析】(1)利用公式法或配方法解方程即可;(2)設這個方程的根為x1、x2 , 即當x=x1 , x=x2時,y=4,可設拋物線解析式y=a(2x2﹣x﹣8)+4,再將x=2,y=﹣4代入求a即可.
【考點精析】關于本題考查的二次函數的概念和拋物線與坐標軸的交點,需要了解一般地,自變量x和因變量y之間存在如下關系:一般式:y=ax2+bx+c(a≠0,a、b、c為常數),則稱y為x的二次函數;一元二次方程的解是其對應的二次函數的圖像與x軸的交點坐標.因此一元二次方程中的b2-4ac,在二次函數中表示圖像與x軸是否有交點.當b2-4ac>0時,圖像與x軸有兩個交點;當b2-4ac=0時,圖像與x軸有一個交點;當b2-4ac<0時,圖像與x軸沒有交點.才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 內的射線.
內的射線.
![]() 如圖1,若OM平分
如圖1,若OM平分![]() ,ON平分
,ON平分![]() 當射線OB繞點O在
當射線OB繞點O在![]() 內旋轉時,
內旋轉時,![]() ______度
______度![]()
![]() 也是
也是![]() 內的射線,如圖2,若
內的射線,如圖2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,當
,當![]() 繞點O在
繞點O在![]() 內旋轉時,求
內旋轉時,求![]() 的大小.
的大小.
![]() 在
在![]() 的條件下,若
的條件下,若![]() ,當
,當![]() 在
在![]() 繞O點以每秒
繞O點以每秒![]() 的速度逆時針旋轉t秒,如圖3,若
的速度逆時針旋轉t秒,如圖3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題一:如圖1,已知A,C兩點之間的距離為16 cm,甲,乙兩點分別從相距3cm的A,B兩點同時出發到C點,若甲的速度為8 cm/s,乙的速度為6 cm/s,設乙運動時間為x(s), 甲乙兩點之間距離為y(cm).
(1)當甲追上乙時,x = .
(2)請用含x的代數式表示y.
當甲追上乙前,y= ;
當甲追上乙后,甲到達C之前,y= ;
當甲到達C之后,乙到達C之前,y= .
![]()
問題二:如圖2,若將上述線段AC彎曲后視作鐘表外圍的一部分,線段AB正好對應鐘表上的弧AB(1小時的間隔),易知∠AOB=30°.
(1)分針OD指向圓周上的點的速度為每分鐘轉動 cm;時針OE指向圓周上的點的速度為每分鐘轉動 cm.
(2)若從4:00起計時,求幾分鐘后分針與時針第一次重合.

查看答案和解析>>
科目:初中數學 來源: 題型:
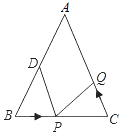
【題目】如圖,已知△ABC中,AB=AC=10cm,BC=8cm,點D為AB的中點.
(1)如果點P在線段BC上以3cm/s的速度由B點向C點運動,同時,點Q在線段CA上由C點向A點運動.
①若點Q的運動速度與點P的運動速度相等,經過1s后,△BPD與△CQP是否全等,請說明理由;
②若點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
(2)若點Q以②中的運動速度從點C出發,點P以原來的運動速度從點B同時出發,都逆時針沿△ABC三邊運動,求經過多長時間點P與點Q第一次在△ABC的哪條邊上相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填在相應的大括號中:8,﹣![]() ,+2.8,π,
,+2.8,π,![]() ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……
正數集合{_____ …}
整數集合{_____…}
負分數集合{_____ …}
無理數集合{_____ …}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,不正確的是( )
A. 平方等于本身的數只有![]() 和
和![]() B. 正數的絕對值是它本身,負數的絕對值是它的相反數
B. 正數的絕對值是它本身,負數的絕對值是它的相反數
C. 兩個數的差為正數,至少其中有一個正數 D. 兩個負數,絕對值大的負數反而小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0)交于A,B兩點,且點A的橫坐標為4,
(k>0)交于A,B兩點,且點A的橫坐標為4,

(1)求 k的值;
(2)利用圖形直接寫出不等式![]() x>
x>![]() 的解;
的解;
(3)過原點O的另一條直線l交雙曲線y=![]() (k>0)于P,Q兩點(P點在第一象限),若由點 A,B,P,Q為頂點組成的四邊形面積為 24,求點 P的坐標.
(k>0)于P,Q兩點(P點在第一象限),若由點 A,B,P,Q為頂點組成的四邊形面積為 24,求點 P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+2x+3與x軸交于A,B兩點,與y軸交于點C,點D,C關于拋物線的對稱軸對稱,直線AD與y軸相交于點E.
(1)求直線AD的解析式;
(2)如圖1,直線AD上方的拋物線上有一點F,過點F作FG⊥AD于點G,作FH平行于x軸交直線AD于點H,求△FGH周長的最大值;
(3)如圖2,點M是拋物線的頂點,點P是y軸上一動點,點Q是坐標平面內一點,四邊形APQM是以PM為對角線的平行四邊形,點Q′與點Q關于直線AM對稱,連接M Q′,P Q′.當△PM Q′與□APQM重合部分的面積是APQM面積的 ![]() 時,求APQM面積.
時,求APQM面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經營某種品牌的玩具,購進時的單價是30元,根據市場調查:在一段時間內,銷售單價是40元時,銷售量是600件,而銷售單價每漲1元,就會少售出10件玩具.
(1)不妨設該種品牌玩具的銷售單價為x元(x>40),請你分別用x的代數式來表示銷售量y件和銷售該品牌玩具獲得利潤w元,并把結果填寫在下列橫線上: 銷售單價x(元);
銷售量y(件);
銷售玩具獲得利潤w(元);
(2)在(1)問條件下,若商場獲得了10000元銷售利潤,求該玩具銷售單價x應定為多少元.
(3)在(1)問條件下,若玩具廠規定該品牌玩具銷售單價不低于44元,且商場要完成不少于540件的銷售任務,求商場銷售該品牌玩具獲得的最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com