
如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從B出發沿BA 向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點.點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm .當點Q到達頂點C時,P,Q同時停止運動.設P, Q兩點運動時間為t秒.

(1)當x為何值時,PQ∥BC ?
(2)設四邊形PQCB的面積為y,求y關于t的函數解析式;
(3)四邊形PQCB的面積與△APQ面積比為3:2?若能,求出此時t的值;若不能,請說明理由;
(4)當x為何值時,△AEQ為等腰三角形?
)(1) ;(2)y=
;(2)y= t2-8t+24;(3)四邊形PQCB面積能是△ABC面積的
t2-8t+24;(3)四邊形PQCB面積能是△ABC面積的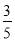 ,此時t的值為5-
,此時t的值為5- ;(4)當t為
;(4)當t為 秒、
秒、 秒、
秒、 秒時,△AEQ為等腰三角形.
秒時,△AEQ為等腰三角形.
【解析】
試題分析:(1)先在Rt△ABC中,由勾股定理求出AB=10,再由BP=t,AQ=2t,得出AP=10-t,然后由PQ∥BC,根據平行線分線段成比例定理得出 ,列出比例式
,列出比例式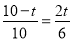 ,求解即可;
,求解即可;
(2)根據S四邊形PQCB=S△ACB-S△APQ= AC•BC-
AC•BC- AP•AQ•sinA,即可得出y關于t的函數關系式;
AP•AQ•sinA,即可得出y關于t的函數關系式;
(3)根據四邊形PQCB面積是△ABC面積的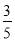 ,列出方程
,列出方程 t2-8t+24=
t2-8t+24=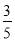 ×24,解方程即可;
×24,解方程即可;
(4)△AEQ為等腰三角形時,分三種情況討論:①AE=AQ;②EA=EQ;③QA=QE,每一種情況都可以列出關于t的方程,解方程即可.
試題解析:(1)Rt△ABC中,∵∠C=90°,BC=8cm,AC=6cm,
∴AB=10cm.
∵BP=t,AQ=2t,
∴AP=AB-BP=10-t.
∵PQ∥BC,
∴ ,
,
∴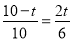 ,
,
解得t= ;
;
(2)∵S四邊形PQCB=S△ACB-S△APQ= AC•BC-
AC•BC- AP•AQ•sinA
AP•AQ•sinA
∴y= ×6×8-
×6×8- ×(10-2t)•2t•
×(10-2t)•2t• =24-
=24- t(10-2t)=
t(10-2t)= t2-8t+24,
t2-8t+24,
即y關于t的函數關系式為y= t2-8t+24;
t2-8t+24;
(3)四邊形PQCB面積能是△ABC面積的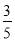 ,理由如下:
,理由如下:
由題意,得
 t2-8t+24=
t2-8t+24=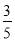 ×24,
×24,
整理,得t2-10t+12=0,
解得t1=5- ,t2=5+
,t2=5+ (不合題意舍去).
(不合題意舍去).
故四邊形PQCB面積能是△ABC面積的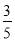 ,此時t的值為5-
,此時t的值為5- ;
;
(4)△AEQ為等腰三角形時,分三種情況討論:
①如果AE=AQ,那么10-2t=2t,解得t= ;
;
②如果EA=EQ,那么(10-2t)× =t,解得t=
=t,解得t= ;
;
③如果QA=QE,那么2t× =5-t,解得t=
=5-t,解得t= .
.
故當t為 秒、
秒、 秒、
秒、 秒時,△AEQ為等腰三角形.
秒時,△AEQ為等腰三角形.
考點:相似形綜合題.


科目:初中數學 來源:2014-2015學年黑龍江省雞西市八年級上學期期中考試數學試卷(解析版) 題型:填空題
已知x=-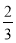 是方程2x+a=
是方程2x+a= +3a的解,則關于m的方程:2am+7=a(3-m)的解,m= 。
+3a的解,則關于m的方程:2am+7=a(3-m)的解,m= 。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省九年級上學期期末模擬考試數學試卷(解析版) 題型:解答題
如圖,一次函數y1=2x+1的圖像與反比例函數y2=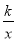 (k為常數,且
(k為常數,且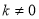 )的圖像都經過點A(m,3)
)的圖像都經過點A(m,3)
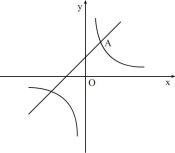
(1)求點A的坐標及反比例函數的表達式
(2)結合圖像直接比較:當x>0時,y1和y2的大小.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省啟東市濱海實驗校共同體九年級上學期第二次質檢數學試卷(解析版) 題型:解答題
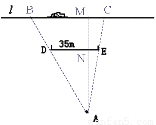
如示意圖,小華家(點A處)和公路(l)之間豎立著一塊35m長且平行于公路的巨型廣告牌(DE).廣告牌擋住了小華的視線,請在圖中畫出視點A的盲區,并將盲區內的那段公路計為BC.一輛以60km/h勻速行駛的汽車經過公路段的時間是3s,已知廣告牌和公路的距離是40m,求小華家到公路的距離.(精確到1m)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市八年級上學期期末模擬數學試卷(解析版) 題型:選擇題
下列說法正確的是( )
A.﹣3的倒數是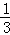
B.﹣2的絕對值是﹣2
C.﹣(﹣5)的相反數是﹣5
D.x取任意實數時, 都有意義
都有意義
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com