
 如圖,等邊△ABC內接于⊙O,P是劣弧
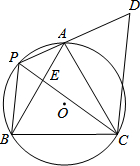
如圖,等邊△ABC內接于⊙O,P是劣弧 上一點(不與A、B重合),將△PBC繞C點順時針旋轉60°,得△DAC,AB交PC于E.則下列結論正確的序號是________.
上一點(不與A、B重合),將△PBC繞C點順時針旋轉60°,得△DAC,AB交PC于E.則下列結論正確的序號是________.
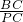 =
=
 上一點(不與A、B重合),
上一點(不與A、B重合), 上一點(不與A、B重合),將△PBC繞C點順時針旋轉60°,
上一點(不與A、B重合),將△PBC繞C點順時針旋轉60°, 的中點時,PC最大,此時三角形面積最大,
的中點時,PC最大,此時三角形面積最大,

 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
 | BC |
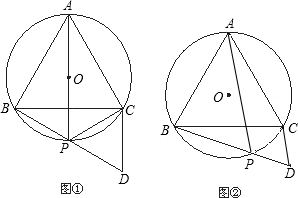 明理由;
明理由;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com