
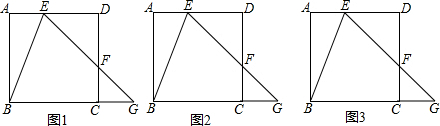
分析 (1)證明:∵根據正方形的性質得到AD∥BG,根據平行線的性質得到∠AEB=∠EBG等量代換得到∠BEG=∠EBG,于是得到結論;
(2)作BQ⊥GE于Q,根據全等三角形的性質得到AB=QB,AE=QE,則BQ=BC,FQ=FC,如何根據線段的和差即可得到結論;
(3)作GH⊥BE于點H,則△BGE是等腰三角形,根據相似三角形的對應邊的比相等即可求解.
解答 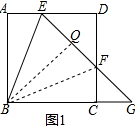 (1)證明:∵四邊形ABCD是正方形,∴AD∥BG,∴∠AEB=∠EBG,∵∠AEB=∠BEG,∴∠BEG=∠EBG,∴BG=EG,∴△BEG為等腰三角形;
(1)證明:∵四邊形ABCD是正方形,∴AD∥BG,∴∠AEB=∠EBG,∵∠AEB=∠BEG,∴∠BEG=∠EBG,∴BG=EG,∴△BEG為等腰三角形;
(2)解:AE+GF=EF.理由如下:
作BQ⊥GE于Q,如圖1,
在△BEA和△BEQ中
$\left\{\begin{array}{l}{∠A=∠BQE}\\{∠AEB=∠QEB}\\{BE=BE}\end{array}\right.$,
∴△BEA≌△BEQ(AAS),
∴AB=QB,AE=QE,
而AB=BC,
∴BQ=BC,
在△BFQ和△BFC中
$\left\{\begin{array}{l}{BQ=BC}\\{BF=BF}\end{array}\right.$,
∴△BFQ≌△BFC(HL),
∴FQ=FC,
∴EF=EQ+FQ=AE+CF;
(3)解:作GH⊥BE于H,如圖2,
在Rt△ABE中,AB=4,AE=1,BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{17}$,
∵△GBE為等腰三角形,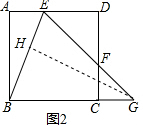
∴BH=EH,
∴BH=$\frac{1}{2}$BE=$\frac{1}{2}$$\sqrt{17}$,
∵∠AEB=∠GBH,
∴Rt△ABE∽Rt△BGH,
∴$\frac{AB}{GH}$=$\frac{AE}{BH}$,即$\frac{4}{GH}$=$\frac{1}{\frac{\sqrt{17}}{2}}$,
∴GH=2 $\sqrt{17}$,
∴S△BEG=$\frac{1}{2}$×BE×GE=$\frac{1}{2}$×$\sqrt{17}$×2 $\sqrt{17}$=17;
∵BG=$\sqrt{B{H}^{2}+G{H}^{2}}$=$\frac{17}{2}$,
∴CG=$\frac{9}{2}$,
∵AE=1AD=AB=4,
∴DE=3,
∵△DEF∽△CGF,
∴$\frac{DE}{CG}=\frac{DF}{CF}$,即$\frac{3}{\frac{9}{2}}=\frac{4-CF}{CF}$,
∴CF=$\frac{12}{5}$,
∴四邊形BEFC的面積=S△BEG-S△CFG=17-$\frac{1}{2}$×$\frac{9}{2}$×$\frac{12}{5}$=$\frac{52}{5}$.
點評 本題考查了四邊形的綜合題:熟練掌握正方形的性質、等腰三角形的性質和全等三角形的判定與性質;會利用勾股定理和相似比進行幾何計算.


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (0,5) | B. | (5,0) | C. | (0,3) | D. | (3,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
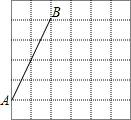 如圖,在每個小正方形的邊長均為1的方格紙中,有線段AB,點A、B均在小正方形的頂點上.
如圖,在每個小正方形的邊長均為1的方格紙中,有線段AB,點A、B均在小正方形的頂點上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com