
【題目】如圖,A、B分別是x軸上位于原點左右兩側的點,點P(2,p)在第一象限,直線PA交y軸于點C(0,3),直線PB交y軸于點D,△AOP的面積為12;
(1)求△COP的面積;
(2)求點A的坐標及p的值;
(3)若△BOP與△DOP的面積相等,求直線BD的函數解析式.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)y=-2x+8.
;(3)y=-2x+8.
【解析】
(1)已知P的橫坐標,即可知道△OCP的邊OC上的高長,利用三角形的面積公式即可求解;
(2)求得△AOC的面積,即可求得A的坐標,利用待定系數法即可求得AP的解析式,把x=2代入解析式即可求得p的值;
(3)利用三角形面積公式由S△BOP=S△DOP,PB=PD,即點P為BD的中點,則可確定B點坐標為(4,0),D點坐標為(0,8),然后利用待定系數法確定直線BD的解析式.
(1)作PE⊥y軸于E,

∵P的橫坐標是2,則PE=2.
∴S△COP=![]() OCPE=
OCPE=![]() ×3×2=3;
×3×2=3;
(2)∴S△AOC=S△AOP-S△COP=12-3=9,
∴S△AOC=![]() OAOC=9,即
OAOC=9,即![]() ×OA×3=9,
×OA×3=9,
∴OA=6,
∴A的坐標是(-6,0).
設直線AP的解析式是y=kx+b,則
![]() ,
,
解得:![]() .
.
則直線AP的解析式是y=![]() x+3.
x+3.
當x=2時,y=4,即p=4;
(3)∵S△BOP=S△DOP,
∴PB=PD,即點P為BD的中點,
∴B點坐標為(4,0),D點坐標為(0,8),
設直線BD的解析式為y=mx+n,
把B(4,0),D(0,8)代入得
![]() ,解得
,解得![]() ,
,
∴直線BD的解析式為:y=-2x+8.


科目:初中數學 來源: 題型:
【題目】已知:如圖,在ABCD中,點E、F分別在AD、BC上,EF與BD相交于點O,AE=CF.
(1)求證:OE=OF;
(2)連接BE、DF,若BD平分∠EBF,試判斷四邊形EBFD的形狀,并給予證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在給定的一張平行四邊形紙片上作一個菱形.甲、乙兩人的作法如下:
甲:連接AC,作AC的垂直平分線MN分別交AD,AC,BC于M,O,N,連接AN,CM,則四邊形ANCM是菱形.
乙:分別作∠A,∠B的平分線AE,BF,分別交BC,AD于E,F,連接EF,則四邊形ABEF是菱形.
根據兩人的作法可判斷

A.甲正確,乙錯誤 B.乙正確,甲錯誤 C.甲、乙均正確 D.甲、乙均錯誤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區有一片樹林,不僅樹種相同,而且排列有序,如果用平面直角坐標系來表示每一棵的具體位置,從第一棵樹開始依次表示為(1,0)→(2,0)→(2,1)→(3,2)→(3,1)→(3,0)→(4.0)→……,則第100棵樹的位置是____.
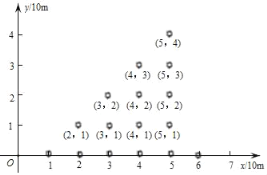
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,x=![]() 是該拋物線的對稱軸,根據圖中所提供的信息,請寫出有關a,b,c的四條結論,并簡要說明理由.
是該拋物線的對稱軸,根據圖中所提供的信息,請寫出有關a,b,c的四條結論,并簡要說明理由.
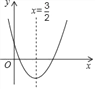
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是正方形ABCD的邊DC上一點,把△ADE順時針旋轉△ABF的位置.
(1)旋轉中心是點 ,旋轉角度是 度;
(2)若連結EF,則△AEF是 三角形;并證明;
(3)若四邊形AECF的面積為25,DE=2,求AE的長.
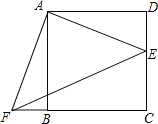
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠計劃生產![]() 兩種產品共10件,其生產成本和銷售價如下表所示:
兩種產品共10件,其生產成本和銷售價如下表所示:
產品 |
|
|
成本(萬元/件) | 3 | 5 |
售價(萬元/件) | 4 | 7 |
(1)若工廠計劃獲利14萬元,則應分別生產![]() 兩種產品多少件?
兩種產品多少件?
(2)若工廠投入資金不多于44萬元,且獲利不少于14萬元,則工廠有哪些生產方案?
(3)在第(2)的條件下,哪種方案獲利最大;最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖一:![]() 中,
中,![]() 平分
平分![]() ,CO平分外角
,CO平分外角![]() .
.
(1)①若![]() ,則
,則![]() 的度數為________.
的度數為________.
②若![]() ,則
,則![]() 的度數為________.
的度數為________.
(2)試寫出![]() 與
與![]() 的關系,并加以證明.
的關系,并加以證明.
(3)解決問題,如圖二,![]() 平分
平分![]() ,
,![]() 平分
平分![]() , 依此類推,
, 依此類推,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() , 依此類推,
, 依此類推,![]() 平分
平分![]() ,若
,若![]() ,請根據第(2)間中得到的結論直接寫出
,請根據第(2)間中得到的結論直接寫出![]() 的度數為________.
的度數為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織部分學參加安全知識競賽,并將成績整理后繪制成直方圖,圖中從左至右前四組的百分比分別是4%,12%,40%,28%,第五組的頻數是8.則:①參加本次競賽的學生共有100人;②第五組的百分比為16%;③成績在70-80分的人數最多;④80分以上的學生有14名;其中正確的個數有( )
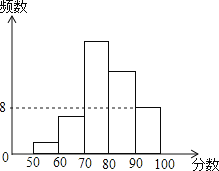
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com