
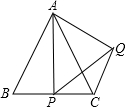
 如圖△ABC為等邊三角形,P為BC上一點,△APQ為等邊三角形.
如圖△ABC為等邊三角形,P為BC上一點,△APQ為等邊三角形. ,
,
 (180°-∠PCQ)=
(180°-∠PCQ)= ×(180°-60°-60°)=30°,
×(180°-60°-60°)=30°,

 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
 12、如圖,在等邊△ABC中,AC=3,點O在AC上,且AO=1.點P是AB上一點,連接OP,以線段OP為一邊作正△OPD,且O、P、D三點依次呈逆時針方向,當點D恰好落在邊BC上時,則AP的長是
12、如圖,在等邊△ABC中,AC=3,點O在AC上,且AO=1.點P是AB上一點,連接OP,以線段OP為一邊作正△OPD,且O、P、D三點依次呈逆時針方向,當點D恰好落在邊BC上時,則AP的長是查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•香坊區三模)如圖,在等邊△ABC中,點D、E分別為AB、AC邊的中點,點F為BC邊上一點,CF=1,連接DF,以DF為邊作等邊△DFG,連接AG,且∠DAG=90°,則線段EF的長為
(2012•香坊區三模)如圖,在等邊△ABC中,點D、E分別為AB、AC邊的中點,點F為BC邊上一點,CF=1,連接DF,以DF為邊作等邊△DFG,連接AG,且∠DAG=90°,則線段EF的長為| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABC為等邊三角形,以AB為邊向形外作△ABD,使∠ADB=120°,再以點C為旋轉中心把△CBD旋轉到△CAE,則下列結論:①D、A、E三點共線;②DC平分∠BDA;③∠E=∠BAC;④DC=DB+DA,其中正確的有( )
如圖,△ABC為等邊三角形,以AB為邊向形外作△ABD,使∠ADB=120°,再以點C為旋轉中心把△CBD旋轉到△CAE,則下列結論:①D、A、E三點共線;②DC平分∠BDA;③∠E=∠BAC;④DC=DB+DA,其中正確的有( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在等邊△ABC中,AC=3,點O在AC上,且AO=1.點P是AB上一點,連接OP,以線段OP為一邊作正△OPD,且O、P、D三點依次呈逆時針方向,當點D恰好落在邊BC上時,則AP的長是( )
如圖,在等邊△ABC中,AC=3,點O在AC上,且AO=1.點P是AB上一點,連接OP,以線段OP為一邊作正△OPD,且O、P、D三點依次呈逆時針方向,當點D恰好落在邊BC上時,則AP的長是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com