
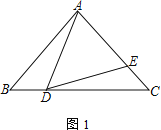
【題目】已知:△ABC中,點D為邊BC上一點,點E在邊AC上,且∠ADE=∠B
(1) 如圖1,若AB=AC,求證:![]() ;
;
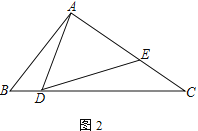
(2) 如圖2,若AD=AE,求證:![]() ;
;
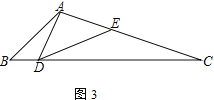
(3) 在(2)的條件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,則AB=____________.
,則AB=____________.
【答案】![]()
【解析】分析:(1)![]()
![]()
∠ADE=∠B,可得![]()
![]() 根據等邊對等角得到
根據等邊對等角得到![]()
△BAD∽△CDE,根據相似三角形的性質即可證明.
(2) 在線段AB上截取DB=DF,證明△AFD∽△DEC,根據相似三角形的性質即可證明.
(3) 過點E作EF⊥BC于F,根據tan∠BAD=tan∠EDF=![]() ,設EF=x,DF=2x,則DE=
,設EF=x,DF=2x,則DE=![]() ,證明△EDC∽△GEC,求得
,證明△EDC∽△GEC,求得![]() ,根據CE2=CD·CG,求出CD=
,根據CE2=CD·CG,求出CD=![]() ,
,
根據△BAD∽△GDE,即可求出![]() 的長度.
的長度.
詳解:(1) ![]()
![]()
∠ADE=∠B,可得![]()
![]()
![]()
![]()
∵△BAD∽△CDE,
∴![]() ;
;
(2) 在線段AB上截取DB=DF
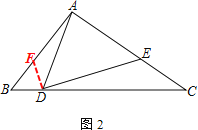
∴∠B=∠DFB=∠ADE
∵AD=AE ∴∠ADE=∠AED ∴∠AED=∠DFB,
同理:∵∠BAD+∠BDA=180°-∠B,∠BDA+∠CDE=180°-∠ADE
∴∠BAD=∠CDE
∵∠AFD=180°-∠DFB,∠DEC=180°-∠AED
∴∠AFD=∠DEC ,
∴△AFD∽△DEC,
∴![]()
(3) 過點E作EF⊥BC于F
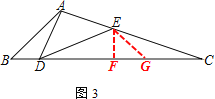
∵∠ADE=∠B=45°
∴∠BDA+∠BAD=135°,∠BDA+∠EDC=135°
∴∠BAD=∠EBC(三等角模型中,這個始終存在)
∵tan∠BAD=tan∠EDF=![]()
∴設EF=x,DF=2x,則DE=![]() ,
,
在DC上取一點G,使∠EGD=45°,
∴△BAD∽△GDE,
∵AD=AE∴∠AED=∠ADE=45°,
∵∠AED=∠EDC+∠C=45°,∠C+∠CEG=45°,∴∠EDC=∠GEC,
∴△EDC∽△GEC,∴![]() ∴
∴![]() ,
,![]()
又CE2=CD·CG,
∴42=CD·![]() ,CD=
,CD=![]() ,
,
∴![]() ,解得
,解得![]()
∵△BAD∽△GDE
∴![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖所示的長方體,已知它的長為4cm,寬為3cm,高為5cm

(1)求此長方體所有棱長的和;
(2)若它是一個無上蓋的精致包裝盒,制作這種包裝盒的紙每平方厘米是0.1元,問制作10個這樣的包裝盒共需多少元?(不考慮接縫之間的材料)
查看答案和解析>>
科目:初中數學 來源: 題型:
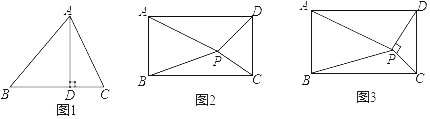
【題目】(幾何背景)如圖1,AD為銳角△ABC的高,垂足為D.求證:AB2﹣AC2=BD2﹣CD2
(知識遷移)如圖2,矩形ABCD內任意一點P,連接PA、PB、PC、PD,請寫出PA、PB、PC、PD之間的數量關系,并說明理由.
(拓展應用)如圖3,矩形ABCD內一點P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c滿足a2﹣b2=![]() c2,則
c2,則![]() 的值為 (請直接寫出結果)
的值為 (請直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的坐標分別為A(﹣3,5),B(﹣4,2),C(﹣1,4)(注:每個方格的邊長均為1個單位長度).
(1)將△ABC沿著水平方向向右平移6個單位得△A1B1C1,請畫出△A1B1C1;
(2)作出將△ABC關于O點成中心對稱的△A2B2C2,并直接寫出的坐標;
(3)△A1B1C1與△A2B2C2是否成中心對稱?若是,請寫出對稱中心的坐標;若不是,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
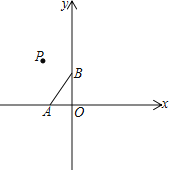
【題目】已知:平面直角坐標系中,點A(-2,0)、B(0,3),點P為第二象限內一點
(1) 如圖,將線段AB繞點P旋轉180°得線段CD,點A與點C對應,試畫出圖形;
(2) 若(1)中得到的點C、D恰好在同一個反比例函數![]() 的圖象上,試求直線BC的解析式;
的圖象上,試求直線BC的解析式;
(3) 若點Q(m,n)為第四象限的一點,將線段AB繞點Q順時針旋轉90°到點E、F.若點E、F恰好在同一個反比例函數的圖象上,試直接寫出m、n之間的關系式__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖正方形ABCD中,點E、F分別在CD、BC邊上,△AEF是等邊三角形.以下結論:①EC=FC;②∠AED=75°;③AF=![]() CE;④EF的垂直平分線是直線AC.正確結論個數有( )個.
CE;④EF的垂直平分線是直線AC.正確結論個數有( )個.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班級準備購買一些獎品獎勵春季運動會表現突出的同學,獎品分為甲、乙兩種,已知,購買一個甲獎品比一個乙獎品多用20元,若用400元購買甲獎品的個數是用160元購買乙獎品個數的一半.
(1)求購買一個甲獎品和一個乙獎品各需多少元?
(2)經商談,商店決定給予該班級每購買甲獎品3個就贈送一個乙獎品的優惠,如果該班級需要乙獎品的個數是甲獎品的2倍還多8個,且該班級購買兩種獎項的總費用不超過640元,那么該班級最多可購買多少個甲獎品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖![]() 是一個可以自由轉動的轉盤,被分成了面積相等的三個扇形,分別標有數
是一個可以自由轉動的轉盤,被分成了面積相等的三個扇形,分別標有數![]() ,
, ![]() ,
, ![]() ,甲轉動一次轉盤,轉盤停止后指針指向的扇形內的數記為
,甲轉動一次轉盤,轉盤停止后指針指向的扇形內的數記為![]() (如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一扇形為止).圖
(如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一扇形為止).圖![]() 是背面完全一樣、牌面數字分別是
是背面完全一樣、牌面數字分別是![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四張撲克牌,把四張撲克牌背面朝上,洗勻后放在桌面上,乙隨機抽出一張牌的牌面數字記為
的四張撲克牌,把四張撲克牌背面朝上,洗勻后放在桌面上,乙隨機抽出一張牌的牌面數字記為![]() .計算
.計算![]() 的值.
的值.


(![]() )用樹狀圖或列表法求
)用樹狀圖或列表法求![]() 的概率.
的概率.
(![]() )甲乙兩人玩游戲,規定:當
)甲乙兩人玩游戲,規定:當![]() 是正數時,甲勝;否則,乙勝,你認為這個游戲規則對甲乙雙方公平嗎?請說明理由.
是正數時,甲勝;否則,乙勝,你認為這個游戲規則對甲乙雙方公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
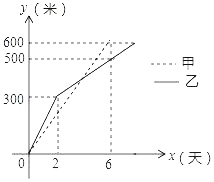
【題目】甲、乙兩工程隊分別同時開挖兩條600米長的管道,所挖管道長度y(單位:米)與挖掘時間x(單位:天)之間的關系如圖所示,則下列說法中:①甲隊每天挖100米;②乙隊開挖兩天后,每天挖50米;③當x=4時,甲、乙兩隊所挖管道長度相同;④甲隊比乙隊提前2天完成任務.正確的是_____(直接填序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com