
【題目】在平面直角坐標系中,A、B、C三點的坐標分別為:A(1,4)、B(0,3)、C(3,0),若P為x軸上一點,且∠BPC=2∠ACB,則點P的坐標為_____.
【答案】(﹣4,0)或(4,0).
【解析】
由已知可得△ABC是直角三角形,作△ABC關于BC的軸對稱圖形,得到△BCN,過點A作AM⊥NC,由三角形ANC面積關系,可得![]() AMNC=
AMNC=![]() 2ABBC,AM=
2ABBC,AM=![]() ,MC=
,MC=![]() ,tan∠ACN=tan2∠ACB=
,tan∠ACN=tan2∠ACB=![]() ,tan∠BPC=
,tan∠BPC=![]() ,所以OP=4.
,所以OP=4.
解:如圖,∵A(1,4)、B(0,3)、C(3,0),
∴AB=![]() ,BC=3
,BC=3![]() ,AC=2
,AC=2![]() ,△ABC是直角三角形,∠ABC=90°,
,△ABC是直角三角形,∠ABC=90°,
作△ABC關于BC的軸對稱圖形,得到△BCN,過點A作AM⊥NC,
由三角形ANC面積關系,可得
![]() AMNC=
AMNC=![]() 2ABBC,
2ABBC,
∴2![]() AM=2×
AM=2×![]() ×3
×3![]() ,
,
∴AM=![]() ,
,
∴MC=![]() ,
,
∴tan∠ACN=tan2∠ACB=![]() ,
,
∵∠BPC=2∠ACB,
∴tan∠BPC=![]() ,
,
∴PO=4,
∴P(﹣4,0)或P(4,0),
故答案為(﹣4,0)或(4,0).



科目:初中數學 來源: 題型:
【題目】在初中階段的函數學習中,我們經歷了“確定函數的表達式一一利用函數圖象研究其性質一一運用函數解決問題”的學習過程.在畫函數圖象時,我們通過描點或平移的方法畫出了所學的函數圖象.同時,我們也學習了絕對值的意義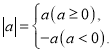 結合上面經歷的學習過程,現在來解決下面的問題:在函數
結合上面經歷的學習過程,現在來解決下面的問題:在函數![]() 中,當
中,當![]() 時,
時,![]() .
.
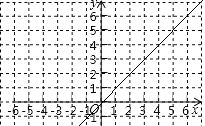
(1)求這個函數的表達式;
(2)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象并寫出這個函數的一條性質;
(3)已如函數![]() 的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式
的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
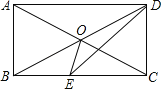
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ABC=∠ADC,對角線AC、BD交于點O,AO=BO,DE平分∠ADC交BC于點E,連接OE.
(1)求證:四邊形ABCD是矩形;
(2)若AB=2,求△OEC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某家具商場計劃購進某種餐桌、餐椅進行銷售,有關信息如表:
原進價(元/張) | 零售價(元/張) | 成套售價(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元購進的餐桌數量與用160元購進的餐椅數量相同.
(1)求表中a的值;
(2)若該商場購進餐椅的數量是餐桌數量的5倍還多20張,且餐桌和餐椅的總數量不超過200張.該商場計劃將一半的餐桌成套(一張餐桌和四張餐椅配成一套)銷售,其余餐桌、餐椅以零售方式銷售.請問怎樣進貨,才能獲得最大利潤?最大利潤是多少?
(3)由于原材料價格上漲,每張餐桌和餐椅的進價都上漲了10元,但銷售價格保持不變.商場購進了餐桌和餐椅共200張,應怎樣安排成套銷售的銷售量(至少10套以上),使得實際全部售出后,最大利潤與(2)中相同?請求出進貨方案和銷售方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
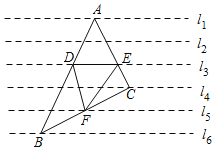
【題目】如圖,一組等距的平行線,點A、B、C分別在直線l1、l6、l4上,AB交l3于點D,AC交l3于點E,BC交于l5點F,若△DEF的面積為1,則△ABC的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AM∥BN,C是BN上一點, BD平分∠ABN且過AC的中點O,交AM于點D,DE⊥BD,交BN于點E.

(1)求證:△ADO≌△CBO.
(2)求證:四邊形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
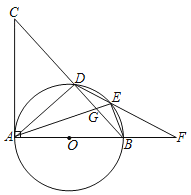
【題目】如圖,AB是⊙O的直徑,AC⊥AB,BC交⊙O于點D,點E在劣弧BD上,DE的延長線交AB的延長線于點F,連接AE交BD于點G.
(1)求證:∠AED=∠CAD;
(2)若點E是劣弧BD的中點,求證:ED2=EGEA;
(3)在(2)的條件下,若BO=BF,DE=2,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受國內外復雜多變的經濟環境影響,去年1至7月,原材料價格一路攀升,長沙市某服裝廠每件衣服原材料的成本y1(元)與月份x(1≤x≤7,且x為整數)之間的函數關系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,隨著經濟環境的好轉,原材料價格的漲勢趨緩,每件原材料成本y2(元)與月份x的函數關系式為y2=x+62(8≤x≤12,且x為整數).
(1)請觀察表格中的數據,用學過的函數相關知識求y1與x的函數關系式.
(2)若去年該衣服每件的出廠價為100元,生產每件衣服的其他成本為8元,該衣服在1至7月的銷售量p1(萬件)與月份x滿足關系式p1=0.1x+1.1(1≤x≤7,且x為整數); 8至12月的銷售量p2(萬件)與月份x滿足關系式p2=﹣0.1x+3(8≤x≤12,且x為整數),該廠去年哪個月利潤最大;并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設等邊三角形的內切圓半徑為![]() 外接圓半徑為
外接圓半徑為![]() ,平面內任意一點
,平面內任意一點![]() 到等邊三角形中心的距離為
到等邊三角形中心的距離為![]() 若滿足
若滿足![]() 則稱點
則稱點![]() 叫做等邊三角形的中心關聯點.在平面直角坐標系
叫做等邊三角形的中心關聯點.在平面直角坐標系![]() 中,等邊
中,等邊![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() .
.
(1)①等邊![]() 中心的坐標為 ;
中心的坐標為 ;
②已知點![]() 在
在![]() 中,是等邊
中,是等邊![]() 的中心關聯點的是 ;
的中心關聯點的是 ;
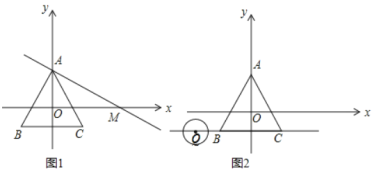
(2)如圖1,過點![]() 作直線交
作直線交![]() 軸正半軸于
軸正半軸于![]() 使
使![]() .
.
①若線段![]() 上存在等邊
上存在等邊![]() 的中心關聯點
的中心關聯點![]() 求
求![]() 的取值范圍;
的取值范圍;
②將直線![]() 向下平移得到直線
向下平移得到直線![]() 當
當![]() 滿足什么條件時,直線
滿足什么條件時,直線![]() 上總存在等邊
上總存在等邊![]() 的中心關聯點;
的中心關聯點;
(3)如圖2,點![]() 為直線
為直線![]() 上一動點,
上一動點,![]() 的半徑為
的半徑為![]() 當
當![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位的速度向右移動,運動時間為
個單位的速度向右移動,運動時間為![]() 秒.是否存在某一時刻
秒.是否存在某一時刻![]() 使得
使得![]() 上所有點都是等邊
上所有點都是等邊![]() 的中心關聯點?如果存在,請直接寫出所有符合題意的
的中心關聯點?如果存在,請直接寫出所有符合題意的![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com