
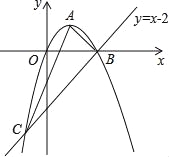
【題目】(2016廣西省南寧市第24題)如圖,已知拋物線經過原點O,頂點為A(1,1),且與直線y=x﹣2交于B,C兩點.
(1)求拋物線的解析式及點C的坐標;
(2)求證:△ABC是直角三角形;
(3)若點N為x軸上的一個動點,過點N作MN⊥x軸與拋物線交于點M,則是否存在以O,M,N為頂點的三角形與△ABC相似?若存在,請求出點N的坐標;若不存在,請說明理由.
【答案】(1)、y=﹣x2+2x;C(-1,-3);(2)、證明過程見解析;(3)、(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0)
,0)或(﹣1,0)或(5,0)
【解析】
試題分析:(1)、可設頂點式,把原點坐標代入可求得拋物線解析式,聯立直線與拋物線解析式,可求得C點坐標;(2)、分別過A、C兩點作x軸的垂線,交x軸于點D、E兩點,結合A、B、C三點的坐標可求得∠ABO=∠CBO=45°,可證得結論;(3)、設出N點坐標,可表示出M點坐標,從而可表示出MN、ON的長度,當△MON和△ABC相似時,利用三角形相似的性質可得![]() =
=![]() 或
或![]() =
=![]() ,可求得N點的坐標.
,可求得N點的坐標.
試題解析:(1)、∵頂點坐標為(1,1), ∴設拋物線解析式為y=a(x﹣1)2+1,
又拋物線過原點, ∴0=a(0﹣1)2+1,解得a=﹣1, ∴拋物線解析式為y=﹣(x﹣1)2+1, 即y=﹣x2+2x,
聯立拋物線和直線解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(2,0),C(﹣1,﹣3);
(2)、如圖,分別過A、C兩點作x軸的垂線,交x軸于點D、E兩點,
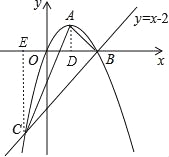
則AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3, ∴∠ABO=∠CBO=45°,即∠ABC=90°, ∴△ABC是直角三角形;
(3)、假設存在滿足條件的點N,設N(x,0),則M(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|, 由(2)在Rt△ABD和Rt△CEB中,可分別求得AB=![]() ,BC=3
,BC=3![]() ,
,
∵MN⊥x軸于點N ∴∠ABC=∠MNO=90°, ∴當△ABC和△MNO相似時有![]() =
=![]() 或
或![]() =
=![]() ,
,
①當![]() =
=![]() 時,則有
時,則有![]() =
=![]() ,即|x||﹣x+2|=
,即|x||﹣x+2|=![]() |x|,
|x|,
∵當x=0時M、O、N不能構成三角形, ∴x≠0, ∴|﹣x+2|=![]() ,即﹣x+2=±
,即﹣x+2=±![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,
,
此時N點坐標為(![]() ,0)或(
,0)或(![]() ,0);
,0);
②當![]() =
=![]() 時,則有
時,則有![]() =
=![]() ,即|x||﹣x+2|=3|x|,
,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1, 此時N點坐標為(﹣1,0)或(5,0),
綜上可知存在滿足條件的N點,其坐標為(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
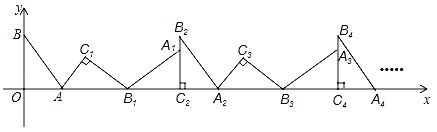
【題目】(2016廣東省梅州市第15題)如圖,在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B、O分別落在點B1、C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去….若點A(![]() ,0),B(0,2),則點B2016的坐標[來為______________.
,0),B(0,2),則點B2016的坐標[來為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個學生從點A向北偏東60方向走40米,到達點B,再從B沿北偏西30方向走 30米,到達點C,此時,恰好在點A的正北方向,則下列說法正確的是( )
A. 點A到BC的距離為30米 B. 點B在點C的南偏東30方向40米處
C. 點A在點B的南偏西60方向30米處 D. 以上都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016湖北省荊州市第25題)閱讀:我們約定,在平面直角坐標系中,經過某點且平行于坐標軸或平行于兩坐標軸夾角平分線的直線,叫該點的“特征線”.例如,點M(1,3)的特征線有:x=1,y=3,y=x+2,y=﹣x+4.

問題與探究:如圖,在平面直角坐標系中有正方形OABC,點B在第一象限,A、C分別在x軸和y軸上,拋物線![]() 經過B、C兩點,頂點D在正方形內部.
經過B、C兩點,頂點D在正方形內部.
(1)直接寫出點D(m,n)所有的特征線;
(2)若點D有一條特征線是y=x+1,求此拋物線的解析式;
(3)點P是AB邊上除點A外的任意一點,連接OP,將△OAP沿著OP折疊,點A落在點A′的位置,當點A′在平行于坐標軸的D點的特征線上時,滿足(2)中條件的拋物線向下平移多少距離,其頂點落在OP上?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為提倡節約用水,采取分段收費.若每戶每月用水不超過20m3 , 每立方米收費2元;若用水超過20m3 , 超過部分每立方米加收1元.小明家5月份交水費64元,則他家該月用水( )m3 .
A.38
B.34
C.28
D.44
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:
(1)只有兩個三角形才能完全重合;
(2)如果兩個圖形全等,它們的形狀和大小一定都相同;
(3)兩個正方形一定是全等形;
(4)邊數相同的圖形一定能互相重合.
其中錯誤命題的個數是( )
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com