【題目】如圖，小巷左右兩側是豎直的墻，一架梯子AC斜靠在右墻，測得梯子頂端距離地面AB＝2米，梯子與地面夾角α的正弦值sinα＝0.8．梯子底端位置不動，將梯子斜靠在左墻時，頂端距離地面2.4米，則小巷的寬度為( )
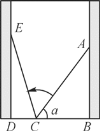
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
科目：初中數學 來源： 題型：
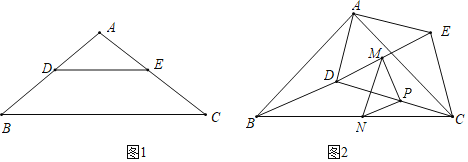
【題目】如圖1，在
中，點D、E分別在AB、AC上，
，
，
求證：
；
若
，把
繞點A逆時針旋轉到圖2的位置，點M，P，N分別為DE，DC，BC的中點，連接MN，PM，PN．
判斷
的形狀，并說明理由；
把繞點A在平面內自由旋轉，若
，
，試問面積是否存在最大值；若存在，求出其最大值
若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
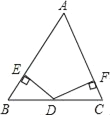
【題目】如圖，在△ABC中，AB＝AC，D是底邊BC的中點，作DE⊥AB于E，DF⊥AC于F
求證：DE＝DF．
證明：∵AB＝AC，∴∠B＝∠C①．
在△BDE和△CDF中，∠B＝∠C，∠BED＝∠CFD，BD＝CD，∴△BDE≌△CDF②．∴DE＝DF③．
（1）上面的證明過程是否正確？若正確，請寫出①、②和③的推理根據．
（2）請你寫出另一種證明此題的方法．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列給出的方程中，屬于一元二次方程的是（ ）
A. x（x﹣1）＝6B. x2+
＝0C. （x﹣3）（x﹣2）＝x2D. ax2+bx+c＝0
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為響應香洲區全面推進書香校園建設的號召，班長小青隨機調查了若干同學一周課外閱讀的時間t（單位：小時），將獲得的數據分成四組，繪制了如下統計圖（A：0＜t≤7，B：7＜t≤14，C：14＜t≤21，D：t＞21），根據圖中信息，解答下列問題：
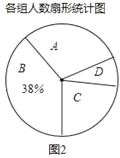
（1）這項工作中被調查的總人數是多少？
（2）補全條形統計圖，并求出表示A組的扇形統計圖的圓心角的度數；
（3）如果小青想從D組的甲、乙、丙、丁四人中先后隨機選擇兩人做讀書心得發言代表，請用列表或樹狀圖的方法求出恰好選中甲的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程x2－(m＋1)x＋
(m2＋1)＝0．
(1)若該方程有實數根，求m的值．
(2)對于函數y1＝x2－(m＋1)x＋(m2＋1)，當x＞1時，y1隨著x的增大而增大．
①求m的范圍．
②若函數y2＝2x＋n與函數
交于y軸上同一點，求n的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
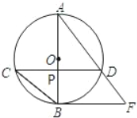
【題目】如圖，AB為⊙O的直徑，弦CD⊥AB，垂足為點P，直線BF與AD的延長線交于點F，且∠AFB=∠ABC．
(1)求證：直線BF是⊙O的切線．
(2)若CD=2
，OP=1，求線段BF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
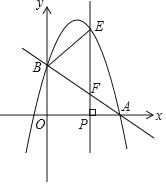
【題目】如圖，在平面直角坐標系中，直線y＝-
x+2分別交x軸、y軸于點A、B，拋物線y＝﹣x2+bx+c經過點A、B．點P是x軸上一個動點，過點P作垂直于x軸的直線分別交拋物線和直線AB于點E和點F．設點P的橫坐標為m．
（1）點A的坐標為 ．
（2）求這條拋物線所對應的函數表達式．
（3）點P在線段OA上時，若以B、E、F為頂點的三角形與△FPA相似，求m的值．
（4）若E、F、P三個點中恰有一點是其它兩點所連線段的中點（三點重合除外），稱E、F、P三點為“共諧點”．直接寫出E、F、P三點成為“共諧點”時m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
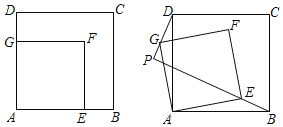
【題目】如圖，在正方形ABCD和正方形AEFG中，邊AE在邊AB上，AB=
，AE=1．將正方形AEFG繞點A逆時針旋轉，設BE的延長線交直線DG于點P，當點P，G第一次重合時停止旋轉．在這個過程中：
（1）∠BPD=______度；
（2）點P所經過的路徑長為______．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
