
【題目】如圖1,在正方形ABCD中,點M、N分別在AD、CD上,若∠MBN=45°,易證MN=AM+CN
⑴ 如圖2,在梯形ABCD中,BC∥AD,AB=BC=CD, 點M、N分別在AD、CD上,若∠MBN=![]() ∠ABC ,試探究線段MN、AM、CN有怎樣的數量關系?請寫出猜想,并給予證明.
∠ABC ,試探究線段MN、AM、CN有怎樣的數量關系?請寫出猜想,并給予證明.
⑵ 如圖3,在四邊形ABCD中,AB=BC,∠ABC+∠ADC=180°,點M、N分別在DA、CD的延長線上,若∠MBN=![]() ∠ABC,試探究線段MN、AM、CN又有怎樣的數量關系?請直接寫出猜想,不需證明.
∠ABC,試探究線段MN、AM、CN又有怎樣的數量關系?請直接寫出猜想,不需證明.

【答案】(1)MN=AM+CN,證明見解析(2)MN=CN-AM
【解析】
(1)先判定梯形ABCD是等腰梯形,根據等腰梯形的性質可得∠A+∠BCD=180°,再把△ABM繞點B順時針旋轉90°,點A與點C重合,點M到達點M′,根據旋轉變換的性質,△ABM和△CBM′全等,根據全等三角形對應邊相等可得AM=CM′,BM=BM′,根據全等三角形對應角相等可得∠A=∠BCM′,∠ABM=∠M′BC,然后證明M′、C、N三點共線,再利用“邊角邊”證明△BMN和△BM′N全等,然后根據全等三角形對應邊相等即可得證;
(2)在∠CBN內部作∠CBM′=∠ABM交CN于點M′,然后證明∠C=∠BAM,再利用“角邊角”證明△ABM和△CBM′全等,根據全等三角形對應邊相等可得AM=CM′,BM=BM′,再證明∠MBN=∠M′BN,利用“邊角邊”證明△MBN和△M′BN全等,根據全等三角形對應邊相等可得MN=M′N,從而得到MN=CN-AM.
(1)MN=AM+CN.
理由如下:
如圖,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM繞點B順時針旋轉使AB邊與BC邊重合,則△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴點M′、C、N三點共線,
∵∠MBN=![]() ∠ABC,
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=![]() ∠ABC,
∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵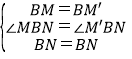 ,
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
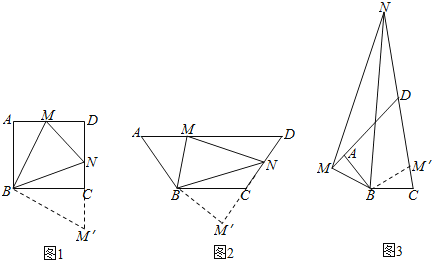
(2)MN=CN-AM.
理由如下:如圖,作∠CBM′=∠ABM交CN于點M′,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠C=360°-180°=180°,
又∵∠BAD+∠BAM=180°,
∴∠C=∠BAM,
在△ABM和△CBM′中,
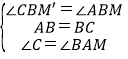 ,
,
∴△ABM≌△CBM′(ASA),
∴AM=CM′,BM=BM′,
∵∠MBN=![]() ∠ABC,
∠ABC,
∴∠M′BN=∠ABC-(∠ABN+∠CBM′)=∠ABC-(∠ABN+∠ABM)=∠ABC-∠MBN=![]() ∠ABC,
∠ABC,
∴∠MBN=∠M′BN,
在△MBN和△M′BN中,
∵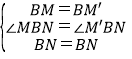 ,
,
∴△MBN≌△M′BN(SAS),
∴MN=M′N,
∵M′N=CN-CM′=CN-AM,
∴MN=CN-AM.


科目:初中數學 來源: 題型:
【題目】兩個邊長分別為![]() 和
和![]() 的正方形如圖放置(圖1),其未疊合部分(陰影)面積為
的正方形如圖放置(圖1),其未疊合部分(陰影)面積為![]() ;若再在圖1中大正方形的右下角擺放一個邊長為
;若再在圖1中大正方形的右下角擺放一個邊長為![]() 的小正方形(如圖2),兩個小正方形疊合部分(陰影)面積為
的小正方形(如圖2),兩個小正方形疊合部分(陰影)面積為![]() .
.



(1)用含![]() 、
、![]() 的代數式分別表示
的代數式分別表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)當![]() 時,求出圖3中陰影部分的面積
時,求出圖3中陰影部分的面積![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
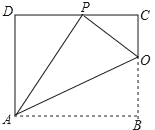
【題目】已知:如圖,矩形ABCD的一條邊AB=10,將矩形ABCD折疊,使得頂點B落在CD邊上的P點處,折痕為AO.
(1)求證:△OCP∽△PDA;
(2)若△OCP與△PDA的面積比為1:4,求邊AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC在平面直角坐標系中的位置如圖所示.將△ABC向右平移6個單位長度,再向下平移4個單位長度得到△A1B1C1.(圖中每個小方格邊長均為1個單位長度).
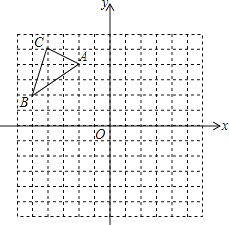
(1)在圖中畫出平移后的△A1B1C1.
(2)直接寫出△A1B1C1.各頂點的坐標:A1____;B1____;C1____.
(3)求出△A1B1C1的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在直線
在直線![]() 上(
上(![]() ,
,![]() 除外),
除外),![]() 的垂線
的垂線![]() 與
與![]() 的垂線
的垂線![]() 交于點
交于點![]() ,研究
,研究![]() 和
和![]() 的數量關系.
的數量關系.
(1)在探究![]() ,
,![]() 的關系時,運用“從特殊到一般”的數學思想,發現當點
的關系時,運用“從特殊到一般”的數學思想,發現當點![]() 是
是![]() 的中點時,只需要取
的中點時,只需要取![]() 邊的中點
邊的中點![]() (如圖),通過推理證明就可以得到
(如圖),通過推理證明就可以得到![]() 的數量關系,請你按照這種思路直接寫出
的數量關系,請你按照這種思路直接寫出![]() 和
和![]() 的數量關系:_____________________
的數量關系:_____________________

(2)當點![]() 是線段
是線段![]() 上(
上(![]() ,
,![]() 除外)任意一點(其它條件不變),上面得到的結論是否仍然成立呢?證明你的結論;
除外)任意一點(其它條件不變),上面得到的結論是否仍然成立呢?證明你的結論;

(3)點![]() 在線段
在線段![]() 的延長線上,上面得到的結論是否仍然成立呢?在下圖中畫出圖形,并證明你的結論.
的延長線上,上面得到的結論是否仍然成立呢?在下圖中畫出圖形,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用因式分解法解下列方程:
(1)(4x﹣1)(5x+7)=0.
(2)3x(x﹣1)=2﹣2x.
(3)(2x+3)2=4(2x+3).
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=kx+6與拋物線y=ax2+bx+c相交于A,B兩點,且點A(1,4)為拋物線的頂點,點B在x軸上.

(1)求拋物線的解析式;
(2)在(1)中拋物線的第三象限圖象上是否存在一點P,使△POB與△POC全等?若存在,求出點P的坐標;若不存在,請說明理由;
(3)若點Q是y軸上一點,且△ABQ為直角三角形,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市銷售一種商品,成本每千克30元,規定每千克售價不低于成本,且不高于70元,經市場調查,每天的銷售量y(千克)與每千克售價x(元)滿足一次函數關系,部分數據如下表:
售價x(元/千克) | 40 | 50 | 60 |
銷售量y(千克) | 100 | 80 | 60 |
(1)求y與x之間的函數表達式;
(2)設商品每天的總利潤為W(元),求W與x之間的函數表達式(利潤=收入成本);
(3)試說明(2)中總利潤W隨售價x的變化而變化的情況,并指出售價為多少元時獲得最大利潤,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com