
 如圖,正方形A1B1B2C1,A2B2B3C2,A3B3B4C3,…,AnBnBn+1Cn,按如圖所示放置,使點A1、A2、A3、A4、…、An在射線OA上,點B1、B2、B3、B4、…、Bn在射線OB上.若∠AOB=45°,OB1=1,圖中陰影部分三角形的面積由小到大依次記作S1,S2,S3,…,Sn,則Sn=________.
如圖,正方形A1B1B2C1,A2B2B3C2,A3B3B4C3,…,AnBnBn+1Cn,按如圖所示放置,使點A1、A2、A3、A4、…、An在射線OA上,點B1、B2、B3、B4、…、Bn在射線OB上.若∠AOB=45°,OB1=1,圖中陰影部分三角形的面積由小到大依次記作S1,S2,S3,…,Sn,則Sn=________. ×20×20,S2=
×20×20,S2= ×21×21,S3=
×21×21,S3= ×22×22,推出Sn=
×22×22,推出Sn= ×2n-1×2n-1,求出即可.
×2n-1×2n-1,求出即可. ×1×1=
×1×1= ×20×20,
×20×20, ×2×2=
×2×2= ×21×21
×21×21 ×4×4=
×4×4= ×22×22,
×22×22, ×8×8=
×8×8= ×23×23,
×23×23, ×2n-1×2n-1=
×2n-1×2n-1=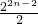 =22n-3.
=22n-3.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
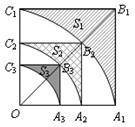 如圖,正方形OA1B1C1的邊長為2,以O為圓心、OA1為半徑作弧A1C1交OB1于點B2,設弧A1C1與邊A1B1、B1C1圍成的陰影部分面積S1;然后以OB2為對角線作正方形OA2B2C2,又以O為圓心、OA2為半徑作弧A2C2交OB2于點B3,設弧A2C2與邊A2B2、B2C2圍成的陰影部分面積為S2;…,按此規律繼續作下去,設弧AnCn與邊AnBn、BnCn圍成的陰影部分面積為Sa.則S1=
如圖,正方形OA1B1C1的邊長為2,以O為圓心、OA1為半徑作弧A1C1交OB1于點B2,設弧A1C1與邊A1B1、B1C1圍成的陰影部分面積S1;然后以OB2為對角線作正方形OA2B2C2,又以O為圓心、OA2為半徑作弧A2C2交OB2于點B3,設弧A2C2與邊A2B2、B2C2圍成的陰影部分面積為S2;…,按此規律繼續作下去,設弧AnCn與邊AnBn、BnCn圍成的陰影部分面積為Sa.則S1=查看答案和解析>>
科目:初中數學 來源:2011-2012學年遼寧省盤錦市四完中九年級(上)第四次月考數學試卷(解析版) 題型:填空題

查看答案和解析>>
科目:初中數學 來源:2009-2010學年浙江省麗水市蓮都區九年級(上)第三次月考數學試卷(解析版) 題型:填空題
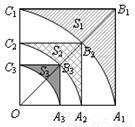
查看答案和解析>>
科目:初中數學 來源:2010年北京市東城區中考數學二模試卷(解析版) 題型:填空題
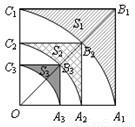
查看答案和解析>>
科目:初中數學 來源:2010年浙江省杭州市蕭山區中考數學模擬試卷47(河莊鎮中 陳國亞)(解析版) 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com