
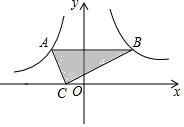
 如圖,將含30°角的三角板ABC放置在坐標系中,此時直角頂點C的坐標是(-1,0),30°角的頂點B在反比例函數y=$\frac{2\sqrt{3}}{x}$位于第一象限內的圖象上,頂點A在反比例函數y=$\frac{k}{x}$位于第二象限內的圖象上,且AB∥x軸,則k的值是( )
如圖,將含30°角的三角板ABC放置在坐標系中,此時直角頂點C的坐標是(-1,0),30°角的頂點B在反比例函數y=$\frac{2\sqrt{3}}{x}$位于第一象限內的圖象上,頂點A在反比例函數y=$\frac{k}{x}$位于第二象限內的圖象上,且AB∥x軸,則k的值是( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -1 | D. | -2 |
分析 作BD⊥x軸于點D,作AE⊥x軸于點E,由AB∥x軸知∠BCD=∠ABC=30°、∠ACE=∠BAC=60°,設點B坐標為(x,$\frac{2\sqrt{3}}{x}$),則BD=$\frac{2\sqrt{3}}{x}$、OD=x,由tan∠BCD=$\frac{BD}{CD}$求得x的值,即可知AE=BD=$\sqrt{3}$,再根據CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1得OE=2,從而得出k的值.
解答 解:如圖,作BD⊥x軸于點D,作AE⊥x軸于點E,
∵AB∥x軸,
∴∠BCD=∠ABC=30°,∠ACE=∠BAC=60°,
設點B坐標為(x,$\frac{2\sqrt{3}}{x}$),
則BD=$\frac{2\sqrt{3}}{x}$,OD=x,
由tan∠BCD=$\frac{BD}{CD}$得$\frac{\sqrt{3}}{3}$=$\frac{\frac{2\sqrt{3}}{x}}{x+1}$,
解得:x=2或x=-3(舍),
∴AE=BD=$\sqrt{3}$,
在Rt△ACE中,∵CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1,
∴OE=2,
則k=-2$\sqrt{3}$,
故選:A
點評 本題考查的是反比例函數圖象上點的坐標特點,熟知反比例函數圖象上各點的坐標一定適合此函數的解析式是解答此題的關鍵.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點B、C、D都在半徑為6的⊙O上,過點C作AC∥BD交OB的延長線于點A,連接CD,已知∠CDB=∠OBD=30°.
如圖,點B、C、D都在半徑為6的⊙O上,過點C作AC∥BD交OB的延長線于點A,連接CD,已知∠CDB=∠OBD=30°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,C,D是線段AB上的兩點,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求線段AB的長.
如圖所示,C,D是線段AB上的兩點,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求線段AB的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 類別 | 頻數 | 頻率 |
| 助人為樂美德少年 | a | 0.20 |
| 自強自立美德少年 | 3 | b |
| 孝老愛親美德少年 | 7 | 0.35 |
| 誠實守信美德少年 | 6 | c |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com