
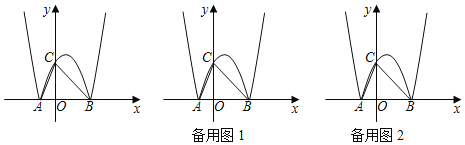
【題目】如圖,在平面直角坐標系中,拋物線y=x2﹣2x﹣3交x軸于A,B兩點(點A在點B的左側),將該拋物線位于x軸上方的曲線記作M,將該拋物線位于x軸下方的部分沿x軸翻折,翻折后所得曲線記作N,曲線N交y軸于點C,連接AC,BC.
(1)求曲線N所在拋物線的函數表達式;
(2)求△ABC外接圓的面積;
(3)點P為曲線M或曲線N上的動點,點Q為x軸上的一個動點,若以點B,C,P,Q為頂點的四邊形是平行四邊形,請直接寫出點Q的坐標;
(4)在直線BC上方的曲線M上確定兩個點D1,D2,使得![]() =
=![]() =S△ABC.并求出點D1,D2的坐標;在曲線M或N上是否存在五個點T1,T2,T3,T4,T5,使得這五個點分別與點B,C圍成的三角形的面積為
=S△ABC.并求出點D1,D2的坐標;在曲線M或N上是否存在五個點T1,T2,T3,T4,T5,使得這五個點分別與點B,C圍成的三角形的面積為![]() ?若存在,直接寫出這五個點T1,T2,T3,T4,T5的坐標;若不存在,請說明理由.
?若存在,直接寫出這五個點T1,T2,T3,T4,T5的坐標;若不存在,請說明理由.
【答案】(1)y=﹣x2+2x+3;(2)5π;(3)Q(1,0)或Q(2﹣![]() ,0)或Q(2+
,0)或Q(2+![]() ,0)時以點B,C,P,Q為頂點的四邊形是平行四邊形;(4)存在,T1(﹣
,0)時以點B,C,P,Q為頂點的四邊形是平行四邊形;(4)存在,T1(﹣![]() ,
,![]() )或T2(
)或T2(![]() ,
,![]() )或T3(
)或T3(![]() ,
,![]() )或T4(
)或T4(![]() ,
,![]() )或T5(
)或T5(![]() ,
,![]() ).
).
【解析】
(1)由N與M圖象下方的部分關于x軸對稱,則可求N的解析式;
(2)求出A、B、C點坐標,分別作BC與AB的垂直平分線交于點O',則O'為△ABC的外接圓,由等腰三角形的性質和勾股定理可求外接圓半徑;
(3)分兩種情況:當P點在M上時,設P(m,m2﹣2m﹣3),Q(n,0),當P點在N上時,設P(m,﹣m2+2m+3),Q(n,0),再在每種情況中分兩種情況①當BQ∥PC,BQ=PC時,②當BP∥CQ,BP=CQ時,利用平行四邊形對角線互相平分的性質,中點重合聯立方程組求解;
(4)由已知可得D1D2所在直線與直線BC平行,D1D2所在直線與直線BC間的距離為2![]() ,設D1D2的直線解析式為y=﹣x+b,由b﹣3=4,可求y=﹣x+7,再與拋物線聯立方程組即可求D1、D2點坐標;T1,T2,T3,T4,T5到直線BC的距離為
,設D1D2的直線解析式為y=﹣x+b,由b﹣3=4,可求y=﹣x+7,再與拋物線聯立方程組即可求D1、D2點坐標;T1,T2,T3,T4,T5到直線BC的距離為![]() ,設與BC平行的直線為y=﹣x+t,則|t﹣3|=
,設與BC平行的直線為y=﹣x+t,則|t﹣3|=![]() ,則五個點分別在直線y=﹣x+
,則五個點分別在直線y=﹣x+![]() 或y=﹣x+
或y=﹣x+![]() 上,再將直線與M、N的解析式聯立即可求坐標.
上,再將直線與M、N的解析式聯立即可求坐標.
解:(1)∵N與M圖象下方的部分關于x軸對稱,
∴N所在函數解析式為y=﹣x2+2x+3;
(2)令x2﹣2x﹣3=0,解得x=﹣1或x=3,
∴A(﹣1,0),B(3,0),
∵曲線N交y軸于點C,
∴C(0,3),
分別作BC與AB的垂直平分線交于點O',則O'為△ABC的外接圓,
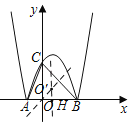
∵Rt△BOC為等腰直角三角形,
∴OO'=OH=O'H=1,
∵HB=2,
∴O'B=![]() ,
,
∵O'B是△ABC外接圓的半徑,
∴△ABC外接圓的面積=5π;
(3)當P點在M上時,設P(m,m2﹣2m﹣3),Q(n,0),
∴m≥3或m≤﹣1;
①當BQ∥PC,BQ=PC時,B、C的中點為(![]() ,
,![]() ),P、Q的中點為(
),P、Q的中點為(![]() ,
,![]() ),
),
∴![]() =
=![]() ,解得m=1+
,解得m=1+![]() 或m=1﹣
或m=1﹣![]() ,
,
![]() =
=![]() ,解得n=2﹣
,解得n=2﹣![]() 或n=2+
或n=2+![]() ,
,
∴Q(2﹣![]() ,0)或Q(2+
,0)或Q(2+![]() ,0);
,0);
②當BP∥CQ,BP=CQ時,B、Q的中點為(![]() ,0),P、C的中點為(
,0),P、C的中點為(![]() ,
,![]() ),
),
∴![]() =0,解得m=0或m=2(都不符合);
=0,解得m=0或m=2(都不符合);
當P點在N上時,設P(m,﹣m2+2m+3),Q(n,0),
∴﹣1≤m≤3,
③當BQ∥PC,BQ=PC時,B、C的中點為(![]() ,
,![]() ),P、Q的中點為(
),P、Q的中點為(![]() ,
,![]() ),
),
∴![]() =
=![]() ,解得m=0或m=2,
,解得m=0或m=2,
![]() =
=![]() ,解得n=3或n=1,
,解得n=3或n=1,
∴Q(1,0)或Q(3,0),
∵Q(3,0)與B(3,0)重合,
∴Q(1,0);
④當BP∥CQ,BP=CQ時,B、Q的中點為(![]() ,0),P、C的中點為(
,0),P、C的中點為(![]() ,
,![]() ),
),
∴![]() =0,解得m=1+
=0,解得m=1+![]() 或m=1﹣
或m=1﹣![]() (都不符合);
(都不符合);
綜上所述:Q(1,0)或Q(2﹣![]() ,0)或Q(2+
,0)或Q(2+![]() ,0)時以點B,C,P,Q為頂點的四邊形是平行四邊形;
,0)時以點B,C,P,Q為頂點的四邊形是平行四邊形;
(4)∵![]() =
=![]() =S△ABC,
=S△ABC,
∴D1D2所在直線與直線BC平行,
∵BC=3![]() ,
,
設A點到BC的距離為h,
∵△ABC的面積=![]() ×3
×3![]() h=
h=![]() ×4×3,
×4×3,
∴h=2![]() ,
,
∴D1D2所在直線與直線BC間的距離為2![]() ,
,
設D1D2的直線解析式為y=﹣x+b,
∴b﹣3=4,
∴b=7,
∴y=﹣x+7,
聯立![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,
,
∴D1(![]() ,
,![]() ),D2(
),D2(![]() ,
,![]() );
);
聯立![]() ,解得x無解;
,解得x無解;
綜上所述:D1(![]() ,
,![]() ),D2(
),D2(![]() ,
,![]() );
);
∵T1,T2,T3,T4,T5與點B,C圍成的三角形的面積為![]() ,
,
∴T1,T2,T3,T4,T5到直線BC的距離為![]() ,
,
設與BC平行的直線為y=﹣x+t,
∴|t﹣3|=![]() ,
,
∴t=![]() 或t=
或t=![]() ,
,
∴y=﹣x+![]() 或y=﹣x+
或y=﹣x+![]() ,
,
當點在M上時,x≥3或x≤﹣1,
聯立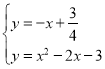 ,解得x=
,解得x=![]() 或x=﹣
或x=﹣![]() ,
,
∴x=﹣![]() ,
,
∴T1(﹣![]() ,
,![]() );
);
聯立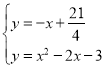 ,解得x=
,解得x=![]() 或x=
或x=![]() ,
,
∴T2(![]() ,
,![]() )或T3(
)或T3(![]() ,
,![]() );
);
當點在N上時,﹣1≤x≤3,
聯立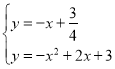 ,解得x=
,解得x=![]() (舍)或x=
(舍)或x=![]() ,
,
∴T4(![]() ,
,![]() );
);
聯立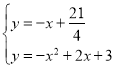 ,解得x=
,解得x=![]() ,
,
∴T5(![]() ,
,![]() );
);
綜上所述:存在五個點符合條件,分別是T1(﹣![]() ,
,![]() )或T2(
)或T2(![]() ,
,![]() )或T3(
)或T3(![]() ,
,![]() )或T4(
)或T4(![]() ,
,![]() )或T5(
)或T5(![]() ,
,![]() ).
).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
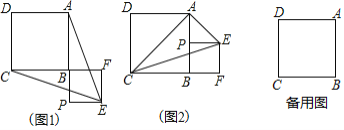
【題目】已知正方形ABCD,P為射線AB上的一點,以BP為邊作正方形BPEF,使點F在線段CB的延長線上,連接EA、EC.
(1)如圖1,若點P在線段AB的延長線上,求證:EA=EC;
(2)若點P在線段AB上,如圖2,當點P為AB的中點時,判斷△ACE的形狀,并說明理由;
(3)在(1)的條件下,將正方形ABCD固定,正方形BPEF繞點B旋轉一周,設AB=4,BP=a,若在旋轉過程中△ACE面積的最小值為4,請直接寫出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
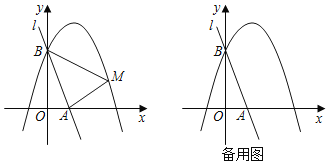
【題目】如圖,直線l:y=﹣3x+3與x軸、y軸分別相交于A、B兩點,拋物線y=ax2﹣2ax+a+4(a<0)經過點B.
(1)求該拋物線的函數表達式;
(2)已知點M是拋物線上的一個動點,并且點M在第一象限內,連接AM、BM,設點M的橫坐標為m,△ABM的面積為S,求S與m的函數表達式,并求出S的最大值;
(3)在(2)的條件下,當S取得最大值時,動點M相應的位置記為點M′.寫出點M′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC的邊長是2,D、E分別為AB、AC的中點,延長BC至點F,使CF=![]() BC,連接CD和EF.
BC,連接CD和EF.
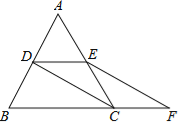
(1)求證:DE=CF;
(2)求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
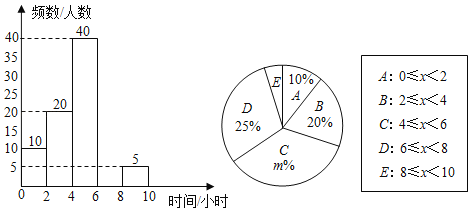
【題目】某中學為了解學生每周的課外閱讀時間情況,隨機抽查了部分學生,對學生每周的課外閱讀時間x(單位:小時)進行分組整理,并制成如圖所示的不完整的頻數分布直方圖和扇形統計圖.
(1)在扇形統計圖中,m= ,E組所對應的扇形的圓心角度數為 ;
(2)E組有3名女同學和2名男同學,學校準備從E組抽2名同學去參加全市舉行的經典誦讀比賽,求抽到1名女同學和1名男同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某校學生對以下四個電視節目:![]() 最強大腦
最強大腦![]() 、
、![]() 中國詩詞大會
中國詩詞大會![]() 、
、![]() 朗讀者
朗讀者![]() 、
、![]() 出彩中國人
出彩中國人![]() 的喜愛情況,隨機抽取了部分學生進行調查,要求每名學生選出并且只能選出一個自己最喜愛的節目,根據調查結果,繪制了如下兩幅不完整的統計圖.
的喜愛情況,隨機抽取了部分學生進行調查,要求每名學生選出并且只能選出一個自己最喜愛的節目,根據調查結果,繪制了如下兩幅不完整的統計圖.

請你根據圖中所提供的信息,完成下列問題:
![]() 本次調查的學生人數為______;
本次調查的學生人數為______;
![]() 在扇形統計圖中,A部分所占圓心角的度數為______;
在扇形統計圖中,A部分所占圓心角的度數為______;
![]() 請將條形統計圖補充完整;
請將條形統計圖補充完整;
![]() 若該校共有3000名學生,估計該校最喜愛
若該校共有3000名學生,估計該校最喜愛![]() 中國詩詞大會
中國詩詞大會![]() 的學生有多少名.
的學生有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一座古拱橋的截面圖,拱橋橋洞的上沿是拋物線形狀,當水面的寬度為10m時,橋洞與水面
的最大距離是5m.
(1)經過討論,同學們得出三種建立平面直角坐標系的方案(如下圖)
你選擇的方案是_____(填方案一,方案二,或方案三),則B點坐標是______,求出你所選方案中的拋物線的表達式;
(2)因為上游水庫泄洪,水面寬度變為6m,求水面上漲的高度.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點E在BC邊上.AE=AB,將線段AC繞點A旋轉到AF的位置.使得∠CAF=∠BAE.連接EF,EF與AC交于點G.

(1)求證:EF =BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
如圖1.在△ABC中,∠A、∠B、∠C所對的邊分別為a、b、c,可以得到:
![]()
證明:過點A作AD⊥BC,垂足為D.
在Rt△ABD中,![]()
∴![]()
∴![]()
同理:![]()
![]()
∴![]()
(1)通過上述材料證明:
![]()
(2)運用(1)中的結論解決問題:
如圖2,在![]() 中,
中,![]() ,求AC的長度.
,求AC的長度.
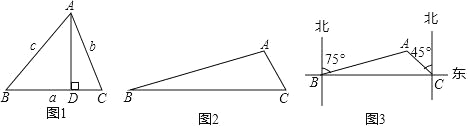
(3)如圖3,為了開發公路旁的城市荒地,測量人員選擇A、B、C三個測量點,在B點測得A在北偏東75°方向上,沿筆直公路向正東方向行駛18km到達C點,測得A在北偏西45°方向上,根據以上信息,求A、B、C三點圍成的三角形的面積.
(本題參考數值:sin15°≈0.3,sin120°≈0.9,![]() ≈1.4,結果取整數)
≈1.4,結果取整數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com