
分別在下列范圍內求函數y=x2-2x-3的最大值或最小值.
(1)0<x<2;(2)2≤x≤3.
|
解:∵y=x2-2x-3=(x-1)2-4, ∴頂點坐標為(1,-4). (1)∵x=1在0<x<2范圍內,且a=1>0, ∴當x=1時,y有最小值,y最小值=-4.在0<x<2范圍內無最大值; (2)∵x=1不在2≤x≤3范圍內,所以函數y=x2-2x-3(2≤x≤3)的圖象是拋物線y=x2-2x-3的一部分.又a-1>0,故拋物線y=x2-2x-3的開口向上,當x>1時,y隨x的增大而增大,當2≤x≤3時,y隨x的增大而增大. 當x=3時,y最大值=32-2×3-3=0. 當x=2時,y最小值=22-2×2-3=-3. 函數y=x2-2x-3(2≤x≤3)的圖象是如下圖所示的實線部分.
思路點撥:先求出拋物線y=x2-2x-3的頂點坐標,然后看頂點的橫坐標是否在所規定的自變量取值范圍內. 評注:本題一定要用數形結合的思想方法,通過觀察、想象才能得出正確答案. |


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
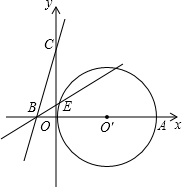 E三點的坐標分別為(-1,0),(0,3)和(0,p),且0<p≤3.
E三點的坐標分別為(-1,0),(0,3)和(0,p),且0<p≤3.查看答案和解析>>
科目:初中數學 來源:新教材完全解讀 九年級數學 (下冊) (配華東師大版新課標) 華東師大版新課標 題型:044
已知二次函數y=x2,分別求出自變量在下列范圍內的函數最值.
(1)x為一切實數;(2)-2≤x≤3;(3)-4≤x≤-1;(4)2≤x≤5.
查看答案和解析>>
科目:初中數學 來源:新教材完全解讀 九年級數學 (下冊) (配華東師大版新課標) 華東師大版新課標 題型:044
分別在下列范圍內求函數y=x2-2x-3的最大值或最小值.
(1)0<x<2;
(2)2≤x≤3.
查看答案和解析>>
科目:初中數學 來源:2002年內蒙古呼和浩特市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com