【題目】如圖，在正方形ABCD中，△BPC是等邊三角形，BP、CP的延長線分別交AD于點E、F，連結BD、DP，BD與CF相交于點H，給出下列結論：①BE＝2AE；②△DFP∽△BPH；③DP2＝PHPC；④FE：BC＝
，其中正確的個數為（ ）
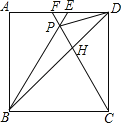
A.1B.2C.3D.4
【答案】D
【解析】
由正方形的性質和相似三角形的判定與性質，即可得出結論．
解：∵△BPC是等邊三角形，
∴BP＝PC＝BC，∠PBC＝∠PCB＝∠BPC＝60°，
在正方形ABCD中，
∵AB＝BC＝CD，∠A＝∠ADC＝∠BCD＝90°
∴∠ABE＝∠DCF＝30°，
∴BE＝2AE；故①正確；
∵PC＝CD，∠PCD＝30°，
∴∠PDC＝75°，
∴∠FDP＝15°，
∵∠DBA＝45°，
∴∠PBD＝15°，
∴∠FDP＝∠PBD，
∵∠DFP＝∠BPC＝60°，
∴△DFP∽△BPH；故②正確；
∵∠PDH＝∠PCD＝30°，∠DPH＝∠DPC，
∴△DPH∽△CPD，
∴
，
∴DP2＝PHPC，故③正確；
∵∠ABE＝30°，∠A＝90°
∴AE＝
AB＝BC，
∵∠DCF＝30°，
∴DF＝DC＝BC，
∴EF＝AE+DF＝
﹣BC，
∴FE：BC＝（2
﹣3）：3
故④正確，
故選：D．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，直線
與雙曲線
（x>0）交于點
．
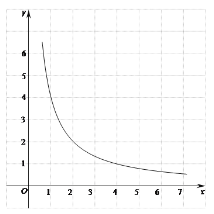
（1）求a，k的值；
（2）已知直線
過點
且平行于直線，點P（m，n）（m>3）是直線上一動點，過點P分別作
軸、
軸的平行線，交雙曲線（x>0）于點
、
，雙曲線在點M、N之間的部分與線段PM、PN所圍成的區域（不含邊界）記為
．橫、縱坐標都是整數的點叫做整點．
①當
時，直接寫出區域內的整點個數；②若區域內的整點個數不超過8個，結合圖象，求m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
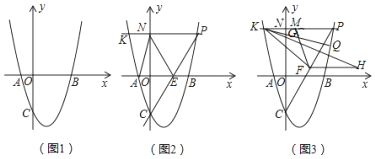
【題目】在平面直角坐標系xOy中，拋物線y＝x2+bx+c交x軸于A（﹣1，0），B（3，0）兩點，交y軸于點C．
（1）如圖1，求拋物線的解析式；
（2）如圖2，點P是第一象限拋物線上的一個動點，連接CP交x軸于點E，過點P作PK∥x軸交拋物線于點K，交y軸于點N，連接AN、EN、AC，設點P的橫坐標為t，四邊形ACEN的面積為S，求S與t之間的函數關系式（不要求寫出自變量t的取值范圍）；
（3）如圖3，在（2）的條件下，點F是PC中點，過點K作PC的垂線與過點F平行于x軸的直線交于點H，KH＝CP，點Q為第一象限內直線KP下方拋物線上一點，連接KQ交y軸于點G，點M是KP上一點，連接MF、KF，若∠MFK＝∠PKQ，MP＝AE+
GN，求點Q坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
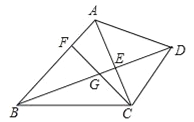
【題目】已知：如圖，在四邊形ABCD中，AB∥CD，對角線AC、BD交于點E，點F在邊AB上，連接CF交線段BE于點G，CG2=GEGD．
（1）求證：∠ACF=∠ABD；
（2）連接EF，求證：EFCG=EGCB．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在“書香校園”活動中，某校為了解學生家庭藏書情況，隨機抽取本校部分學生進行調查，并繪制成部分統計圖表如下：
類別 | 家庭藏書m本 | 學生人數 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根據以上信息，解答下列問題：
（1）該調查的樣本容量為 ，a＝ ；
（2）隨機抽取一位學生進行調查，剛好抽到A類學生的概率是 ；
（3）若該校有2000名學生，請估計全校學生中家庭藏書不少于76本的人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
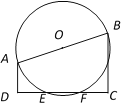
【題目】如圖，梯形ABCD中，AD∥BC，∠ADC=90，AD= 2，BC= 4，
.以AB為直徑作⊙O，交邊DC于E、F兩點.
(1)求證：DE=CF.
(2)求直徑AB的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
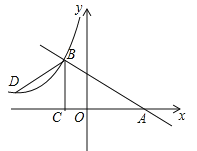
【題目】如圖，已知一次函數y=kx+b的圖象與x軸交于點A，與反比例函數
（x＜0）的圖象交于點B（﹣2，n），過點B作BC⊥x軸于點C，點D（3﹣3n，1）是該反比例函數圖象上一點．
（1）求m的值；
（2）若∠DBC=∠ABC，求一次函數y=kx+b的表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將一副三角板中含有30°角的三角板的直角頂點落在等腰直角三角形的斜邊的中點D處，并繞點D旋轉，兩直角三角板的兩直角邊分別交于點E，F，下列結論：①DE=DF；②S四邊形AEDF=S△BED+S△CFD；③S△ABC=EF2；④EF2=BE2+CF2，其中正確的序號是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市三景區是人們節假日游玩的熱點景區，某學校對九（1）班學生“五一”小長假隨父母到這三個景區游玩的計劃做了全面調查，調查分四個類別，A：三個景區；B：游兩個景區；C：游一個景區；D：不到這三個景區游玩，現根據調查結果繪制了不完全的條形統計圖和扇形統計圖如下：
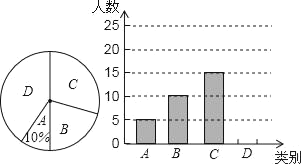
請結合圖中信息解答下列問題：
（1）九（1）班現有學生 人，在扇形統計圖中表示“B類別”的扇形的圓心角的度數為 ；
（2）請將條形統計圖補充完整；
（3）若該校九年級有1000名學生，求計劃“五一”小長假隨父母到這三個景區游玩的學生多少名？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com