
【題目】把代數式通過配湊等手段,得到局部完全平方式,再進行有關運算和解題,這種解題方法叫做配方法.
如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1-1=a2+6a+9-1
=(a+3)2-12=![]()
②M=a2-2a-1,利用配方法求M的最小值.
解:![]()
∵(a-b)2≥0,∴當a=1時,M有最小值-2.
請根據上述材料解決下列問題:
(1)用配方法因式分解:![]() .
.
(2)若![]() ,求M的最小值.
,求M的最小值.
(3)已知x2+2y2+z2-2xy-2y-4z+5=0,求x+y+z的值.
 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度數;
(2)求證:直線AD是線段CE的垂直平分線.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰直角三角板ABC的斜邊AB與量角器的直徑重合,點D是量角器上60°刻度線的外端點,連接CD交AB于點E,則∠CEB的度數為( )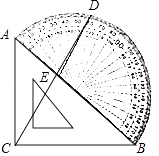
A.60°
B.65°
C.70°
D.75°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘輪船航行到B處時,測得小島A在船的北偏東60°的方向上,輪船從B處繼續向正東方向航行100海里到達C處時,測得小島A在船的北偏東30°的方向上,AD⊥BC于點D,求AD的長.
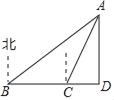
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有兩個不相等的實數根,求k的取值范圍;
(2)若方程的兩根恰好是一個矩形的兩邊長,且k=4,求該矩形的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,∠1=∠2,CF平分∠DCE.
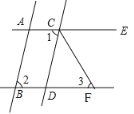
(1)試判斷直線AE與BF有怎樣的位置關系,并說明理由;
(2)若∠1=80°,求∠3的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+bx+ ![]() 經過A(1,0),B(7,0)兩點,交y軸于D點,以AB為邊在x軸上方作等邊三角形ABC.
經過A(1,0),B(7,0)兩點,交y軸于D點,以AB為邊在x軸上方作等邊三角形ABC.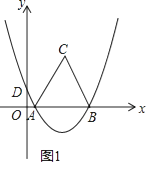
(1)求拋物線的解析式;
(2)在x軸上方的拋物線上是否存在點M,是S△ABM= ![]() S△ABC?若存在,請求出點M的坐標;若不存在,請說明理由;
S△ABC?若存在,請求出點M的坐標;若不存在,請說明理由;
(3)如圖2,E是線段AC上的動點,F是線段BC上的動點,AF與BE相交于點P.
①若CE=BF,試猜想AF與BE的數量關系及∠APB的度數,并說明理由;
②若AF=BE,當點E由A運動到C時,請直接寫出點P經過的路徑長.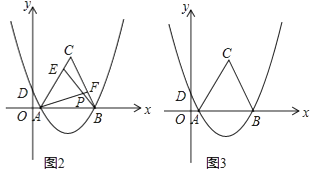
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了搞好對“傳統文化學習”的宣傳活動,對本校部分學生(隨機抽查)進行了一次相關知識了解程度的調查測試(成績分為A、B、C、D、E五個組,x表示測試成績).通過對測試成績的分析,得到如圖所示的兩幅不完整的統計圖.請你根據圖中提供的信息解答以下問題: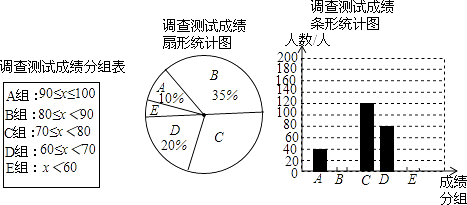
(1)參加調查測試的學生為人;
(2)將條形統計圖補充完整;
(3)本次調查測試成績中的中位數落在組內;
(4)若測試成績在80分以上(含80分)為優秀,該中學共有學生2600人,請你根據樣本數據估計全校學生測試成績為優秀的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長是16,點E在邊AB上,AE=3,點F是邊BC上不與點B,C重合的一個動點,把△EBF沿EF折疊,點B落在B′處.若△CDB′恰為等腰三角形,則DB′的長為 . 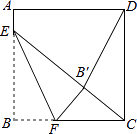
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com