一種產品,原來每件售價是81元,由于求過供,所以產品連續兩次漲價,現售價是100元,則平均每次的增長率為 %(精確到0.1)
【答案】
分析:如果設平均每次的增長率是x,那么這種產品第一次漲價后的價格為81(1+x)元,第二次漲價后的價格為81(1+x)
2元,而此時的價格為100元,根據這個等量關系可以列出方程.
解答:解:設平均每次的增長率為x.
依題意,得81(1+x)
2=100,
解方程,得x
1=

≈11.1%,x
2=-
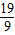
(舍去).
故平均每次的增長率約為11.1%.
點評:本題考查數量平均變化率問題.原來的數量(價格)為a,平均每次增長或降低的百分率為x的話,經過第一次調整,就調整到a(1±x),再經過第二次調整就是a(1±x)(1±x)=a(1±x)
2.增長用“+”,下降用“-”.
