
在直角坐標系中,以原點為圓心,4為半徑作圓,該圓上到直線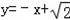
 的距離等于2的點共有( )
的距離等于2的點共有( )
A.1個 B.2個 C.3個 D.4個
D【考點】垂徑定理;坐標與圖形性質;三角形內角和定理;勾股定理;直線與圓的位置關系.
【專題】計算題.
【分析】過O作OH⊥AB,求出O到直線的距離,和圓的半徑比較得出圓于直線相交,且圓心到直線的距離是1,畫出圖形,得出在直線的兩旁到直線的距離等于2的點有4個點,即可得出答案.
【解答】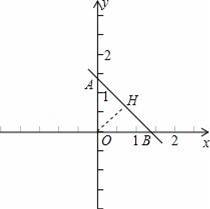

解:過O作OH⊥AB于H,
y=﹣x+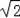
 ,
,
∵當x=0時,y=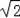
 ,
,
當y=0時,x=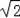
 ,
,
∴AO=OB=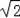
 ,
,
由勾股定理得:AB=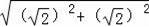
 =2,
=2,
由三角形的面積公式得:AB×OH=AO×OB,
即2OH=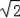
 ×
×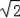
 =2,
=2,
解得:OH=1<4,
即直線與圓相交,
如圖:
在直線的兩旁到直線的距離等于2的點有4個點(E、F、G、N),
故選D.
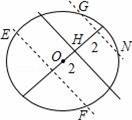

【點評】本題考查了直線與圓的位置關系和三角形的面積的應用,關鍵是求出直線與圓的位置關系和畫出第二個圖形,主要考查學生的理解能力和推理能力,題目有一定的難度,注意:不要漏解啊.


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
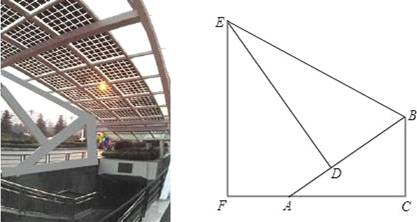
如圖是某地下商業街的入口,數學課外興趣小組的同學打算運用所學的知識測量側面支架的最高點E到地面的距離EF.經測量,支架的立柱BC與地面垂直,即∠BCA=90°,且BC=1.5m,點F、A、C在同一條水平線上,斜桿AB與水平線AC的夾角∠BAC=30°,支撐桿DE⊥AB于點D,該支架的邊BE與AB的夾角∠EBD=60°,又測得AD=1m.請你求出該支架的邊BE及頂端E到地面的距離EF的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
一個口袋中裝有10個紅球和若干個黃球,在不允許將求倒出來數的前提下,為估計袋中黃球的個數,小明采用了如下的方法:每次先從口袋中摸出10個球,求出其中紅球數與10的比值,再把球放回口袋中搖勻,不斷重復上述過程20次,得到紅球與10的比值的平均數為0.4,根據上述數據,估計口袋中大約有( )個黃球.
A.30 B.15 C.20 D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
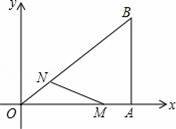
如圖,在直角坐標系中,Rt△OAB的直角頂點A在x軸上,OA=4,AB=3.動點M從點A出發,以每秒1個單位長度的速度,沿AO向終點O移動;同時點N從點O出發,以每秒1.25個單位長度的速度,沿OB向終點B移動.當兩個動點運動了x秒(0<x<4)時,解答下列問題:
(1)求點N的坐標(用含x的代數式表示);
(2)設△OMN的面積是S,求S與x之間的函數表達式;當x為何值時,S有最大值?最大值是多少?
(3)在兩個動點運動過程中,是否存在某一時刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com