某商場欲購進A、B兩種水杯進行銷售.已知每個A種水杯的進價比每個B種水杯的進價貴10元,并且800元購進B種水杯數量是500元購進A種水杯數量的2倍.
(1)求A、B兩種水杯的進價分別是多少元?
(2)該商場計劃按(1)的進價購進A、B兩種水杯共45個,且A、B兩種水杯售價分別定為70元和55元.若該商場計劃購買A、B兩種水杯的費用不超過2000元,全部售出后所得總利潤不低于760元.請你通過計算為該商場設計進貨方案.
【答案】
分析:(1)設A種水杯進價為x元,則B種水杯的進價為x-10,根據題意列出方程式即可求出A、B兩種水杯的進價;
(2)設進A種水杯m個,則B種水杯為45-m個,根據A、B兩種水杯的費用不超過2000元,全部售出后所得總利潤不低于760元,可得出不等式組,解出即可.
解答:解:(1)設A種水杯進價為x元,則B種水杯的進價為x-10,
由題意得:
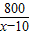
=2×
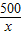
,
化簡得:8x=10x-100,
解得:x=50,則x-10=40,
答:A、B兩種水杯的進價分別是50元、40元.
(2)設進A種水杯m個,則B種水杯為45-m個,
由題意得:
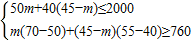
,
解不等式得:

,
故m的取值范圍是:17≤m≤20,
故有四種方案:①A種17個,B種28個;
②A種18個,B種27個;
③A種19個,B種26個;
④A種17個,B種25個.
點評:本題考查了二元一次方程組及一元一次不等式組的應用,解答本題的關鍵是仔細審題,得到題目中的等量關系及不等關系,利用方程和不等式解題,難度一般.

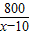 =2×
=2×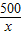 ,
,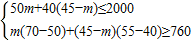 ,
, ,
,

