
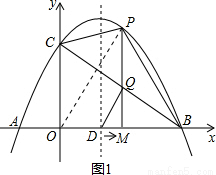
 的圖象與x軸交于A,B兩點,與y軸交于點C,拋物線的對稱軸與x軸交于點D. 點M從O點出發,以每秒1個單位長度的速度向B運動,過M作x軸的垂線,交拋物線于點P,交BC于Q.
的圖象與x軸交于A,B兩點,與y軸交于點C,拋物線的對稱軸與x軸交于點D. 點M從O點出發,以每秒1個單位長度的速度向B運動,過M作x軸的垂線,交拋物線于點P,交BC于Q.
 解:(1)把x=0代入y=-
解:(1)把x=0代入y=- x2+
x2+ x+2得點C的坐標為C(0,2),
x+2得點C的坐標為C(0,2), x2+
x2+ x+2得點B的坐標為B(3,0);
x+2得點B的坐標為B(3,0); ×2×x+
×2×x+ ×3×y,
×3×y, (-
(- x2+
x2+ x+2),
x+2), )2+
)2+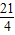 (0≤x≤3);
(0≤x≤3);
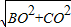 =
=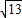 ,
,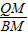 =
=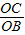 =
= ,
, ,
, ).
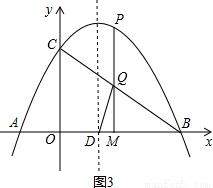
).
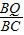 =
=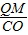 =
=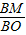 ,
,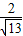 =
=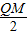 ,
,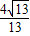 ,
,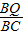 =
=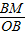 ,
,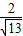 =
=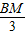 ,
,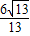 ,
,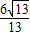 ,
,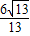 ,
,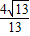 );
); x2+
x2+ x+2,
x+2,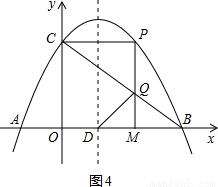
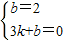 ,
, ,
, x+2,
x+2, x+2,
x+2, x+2與y=-
x+2與y=- x2+
x2+ x+2聯立得:
x+2聯立得: x+2=-
x+2=- x2+
x2+ x+2,
x+2, ,
,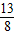 ,
, 時,P點在第2象限,故此時不符合題意,
時,P點在第2象限,故此時不符合題意,

 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:初中數學 來源: 題型:
 如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=
如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•黃岡)如圖,已知拋物線的方程C1:y=-
(2012•黃岡)如圖,已知拋物線的方程C1:y=-| 1 | m |
查看答案和解析>>
科目:初中數學 來源: 題型:
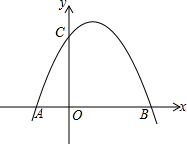 (2013•道外區三模)如圖,已知拋物線y=ax2+bx+c過點A(-1,0)、B(3,0)、C(0,3)
(2013•道外區三模)如圖,已知拋物線y=ax2+bx+c過點A(-1,0)、B(3,0)、C(0,3)查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知拋物線y=ax2-4x+c經過點A(0,-6)和B(3,-9).
如圖,已知拋物線y=ax2-4x+c經過點A(0,-6)和B(3,-9).查看答案和解析>>
科目:初中數學 來源:2010年湘西自治州初中畢業學業考試數學試題 題型:044
如圖,已知拋物線y=ax2-4x+c經過點A(0,-6)和B(3,-9),
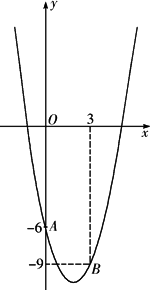
(1)求出拋物線的解析式;
(2)寫出拋物線的對稱軸方程及頂點坐標;
(3)點P(m,m)與點Q均在拋物線上(其中m>0),且這兩點關于拋物線的對稱軸,對稱,求m的值及點Q的坐標;
(4)在滿足(3)的情況下,在拋物線的對稱軸上尋找一點M,使得△QMA的周長最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com