
【題目】已知點M(3,2),拋物線L:y=x2﹣3x+c與x軸從左到右的交點為A,B.
(1)若拋物線L經過點M(3,2),求拋物線L的解析式和頂點坐標;
(2)當2OA=OB時,求c的值;
(3)直線y=x+b經過點M,與y軸交于點N,①求點N的坐標;②若線段MN與拋物線L:y=x2﹣3x+c有唯一公共點,直接寫出正整數c的值.
【答案】(1)y=x2﹣3x+2,頂點坐標為(![]() ,﹣
,﹣![]() );(2)2或﹣18;(3)①(0,﹣1),②1和3
);(2)2或﹣18;(3)①(0,﹣1),②1和3
【解析】
(1)把點M的坐標代入拋物線解析式,利用方程求得c的值;將已得函數解析式配方,可以求得頂點坐標.
(2)設A(![]() ,0),則OB=2OA=2|
,0),則OB=2OA=2|![]() |,需對
|,需對![]() 的正負性進行分類討論.若
的正負性進行分類討論.若![]() >0,則B(2
>0,則B(2![]() ,0),根據點A、B關于拋物線對稱軸對稱可求得
,0),根據點A、B關于拋物線對稱軸對稱可求得![]() 的值,再把點A坐標代入拋物線解析式,解方程即求得c的值.若
的值,再把點A坐標代入拋物線解析式,解方程即求得c的值.若![]() <0,則B(﹣2
<0,則B(﹣2![]() ,0),計算方法與前面一樣.
,0),計算方法與前面一樣.
(3)①利用待定系數法確定一次函數解析式,令x=0即求得點N的坐標.
②由于拋物線開口方向、大小,及對稱軸固定,可把拋物線看作上下平移,再觀察其與線段MN的交點情況.先聯立直線MN和拋物線解析式得到關于x的一元二次方程,計算△=0時c的值,把c的值代回方程組求得直線和拋物線此時的交點,落在線段MN上,說明c的值滿足條件.把拋物線向下平移,剛好過點M時求出c的值,此時直線與拋物線由兩個交點;繼續往下平移拋物線,就變成只有一個交點;一直到拋物線經過點N為止,求c的值,于是得到滿足條件的c的范圍,再取正整數即為所求.
(1)∵拋物線L:y=x2﹣3x+c經過M(3,2)
∴9﹣9+c=2
解得:c=2.
∴y=x2﹣3x+2=(x﹣![]() )2﹣
)2﹣![]()
∴拋物線L的解析式為:y=x2﹣3x+2,頂點坐標為(![]() ,﹣
,﹣![]() )
)
(2)設A(![]() ,0),則OA=|
,0),則OA=|![]() |,OB=2OA=2|
|,OB=2OA=2|![]() |
|
①若![]() >0,則B(2
>0,則B(2![]() ,0)
,0)
∵拋物線對稱軸為直線:x=![]() ,點A、B關于對稱軸對稱
,點A、B關于對稱軸對稱
∴![]() ,即
,即![]()
解得:![]() =1
=1
∴A(1,0)代入拋物線解析式得:1﹣3+c=0
解得:c=2
②若![]() <0,則B(﹣2
<0,則B(﹣2![]() ,0)
,0)
∴![]()
解得:![]() =﹣3
=﹣3
∴A(﹣3,0)代入拋物線解析式得:9+9+c=0
解得:c=﹣18
綜上所述,c的值為2或﹣18.
(3)①∵直線y=x+b經過點M(3,2)
∴3+b=2,解得:b=﹣1
∴直線解析式為y=x﹣1
當x=0時,y=﹣1
∴點N坐標為(0,﹣1)
②聯立直線MN與拋物線解析式得:
![]() 整理得:x2﹣4x+c+1=0
整理得:x2﹣4x+c+1=0
當直線與拋物線只有一個交點時,△=(﹣4)2﹣4(c+1)=0
解得:c=3
∴方程的解為: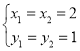
∴此時交點在線段MN上,即c=3滿足“線段MN與拋物線L:y=x2﹣3x+c有唯一公共點”
當拋物線經過點M時,解得c=2,此時拋物線與線段MN有2個公共點
當拋物線往下平移到經過點N時,解得c=﹣1,此時拋物線與線段MN只有交點N
∴當﹣1≤c<2時,拋物線與線段MN只有一個公共點
∴滿足條件的正整數c的值為1和3.


科目:初中數學 來源: 題型:
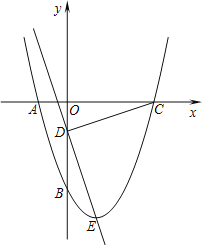
【題目】如圖所示,拋物線y=x2+bx+c經過A、B兩點,A、B兩點的坐標分別為(﹣1,0)、(0,﹣3).
(1)求拋物線的函數解析式;
(2)點E為拋物線的頂點,點C為拋物線與x軸的另一交點,點D為y軸上一點,且DC=DE,求出點D的坐標;
(3)在第二問的條件下,在直線DE上存在點P,使得以C、D、P為頂點的三角形與△DOC相似,請你直接寫出所有滿足條件的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
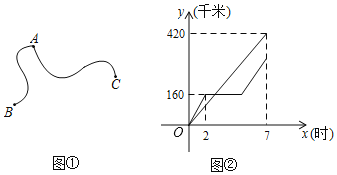
【題目】如圖①,甲、乙兩車同時從A地出發,分別勻速前往B地與C地,甲車到達B地休息一段時間后原速返回,乙車到達C地后立即返回.兩車恰好同時返回A地.圖②是兩車各自行駛的路程y(千米)與出發時間x(時)之間的函數圖象.根據圖象解答下列問題:
(1)甲車到達B地休息了 時;
(2)求甲車返回A地途中y與x之間的函數關系式;
(3)當x為何值時,兩車與A地的路程恰好相同.(不考慮兩車同在A地的情況)
查看答案和解析>>
科目:初中數學 來源: 題型:
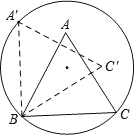
【題目】如圖,正△ABC 的邊長為 2,頂點 B、C 在半徑為![]() 的圓上,頂點 A在圓內,將正△ABC 繞點 B 逆時針旋轉,當點 A 第一次落在圓上時,則點 C 運動的路線長為 (結果保留π);若 A 點落在圓上記做第 1 次旋轉,將△ABC 繞點 A 逆時針旋轉,當點 C 第一次落在圓上記做第 2 次旋轉,再繞 C 將△ABC 逆時針旋轉,當點 B 第一次落在圓上,記做第 3 次旋轉……,若此旋轉下去,當△ABC 完成第 2017 次旋轉時,BC 邊共回到原來位置 次.
的圓上,頂點 A在圓內,將正△ABC 繞點 B 逆時針旋轉,當點 A 第一次落在圓上時,則點 C 運動的路線長為 (結果保留π);若 A 點落在圓上記做第 1 次旋轉,將△ABC 繞點 A 逆時針旋轉,當點 C 第一次落在圓上記做第 2 次旋轉,再繞 C 將△ABC 逆時針旋轉,當點 B 第一次落在圓上,記做第 3 次旋轉……,若此旋轉下去,當△ABC 完成第 2017 次旋轉時,BC 邊共回到原來位置 次.
查看答案和解析>>
科目:初中數學 來源: 題型:
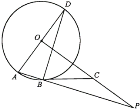
【題目】如圖,AD是⊙O的直徑,AB為⊙O的弦,OP⊥AD,OP與AB的延長線交于點P,過B點的切線交OP于點C.
(1)求證:∠CBP=∠ADB.
(2)若OA=2,AB=1,求線段BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
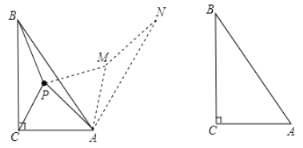
【題目】如圖,在![]() 中,
中,![]() ,點P為
,點P為![]() 內一點,連接PA,PB,PC,求PA+PB+PC的最小值,小華的解題思路,以點A為旋轉中心,將
內一點,連接PA,PB,PC,求PA+PB+PC的最小值,小華的解題思路,以點A為旋轉中心,將![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,那么就將求PA+PB+PC的值轉化為求PM+MN+PC的值,連接CN,當點P,M落在CN上時,此題可解.
,那么就將求PA+PB+PC的值轉化為求PM+MN+PC的值,連接CN,當點P,M落在CN上時,此題可解.
(1)請判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(2)請你參考小華的解題思路,證明PA+PB+PC=PM+MN+PC;
(3)當![]() ,求PA+PB+PC的最小值.
,求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
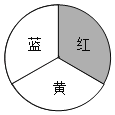
【題目】某商場開業,為了活躍氣氛,用紅、黃、藍三色均分的轉盤設計了兩種抽獎方案,凡來商場消費的顧客都可以選擇一種抽獎方案進行抽獎.
方案一:轉動轉盤一次,指針落在紅色區域可領取一份獎品;
方案二:轉動轉盤兩次,指針落在不同顏色區域可領取一份獎品,你會選擇哪個方案?請用相關的數學知識說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com