
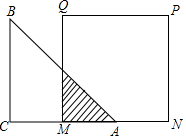
 如圖,已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為10cm,AC與MN在同一直線上,開始時點A與點M重合,讓△ABC向右移動,最后讓點A與點N重合.
如圖,已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為10cm,AC與MN在同一直線上,開始時點A與點M重合,讓△ABC向右移動,最后讓點A與點N重合.分析 (1)根據圖形及題意所述可得出重疊部分是等腰直角三角形,從而根據MA的長度可得出y與x的關系;
(2)根據開始時點A與點M重合,讓△ABC向右移動,最后讓點A與點N重合,可得0≤AM≤10,據此得出自變量的取值范圍;
(3)根據自變量的取值,運用(1)中的函數解析式,通過計算求得重疊部分的面積即可.
解答  解:(1)由題意知,△ABC是等腰直角三角形,∠AMQ=90°,
解:(1)由題意知,△ABC是等腰直角三角形,∠AMQ=90°,
∴重疊部分是等腰直角三角形,
又∵線段AM=x,
∴y=$\frac{1}{2}$x2;
(2)∵開始時點A與點M重合,讓△ABC向右移動,最后讓點A與點N重合,
∴0≤AM≤10,即0≤x≤10,
故自變量x的取值范圍是:0≤x≤10;
(3)當x=MA=4cm時,重疊部分的面積y=$\frac{1}{2}$×42=8(cm2).
點評 本題屬于四邊形綜合題,主要考查了等腰直角三角形的性質,正方形的性質以及二次函數求值的綜合應用,判斷出重疊部分是等腰直角三角形是解決問題的關鍵.等腰直角三角形是一種特殊的三角形,具有所有三角形的性質,還具備等腰三角形和直角三角形的所有性質.


科目:初中數學 來源: 題型:解答題
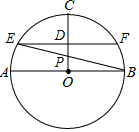 如圖,⊙O中,半徑CO垂直于直徑AB,D為OC的中點,過D作弦EF∥AB,EB與OC交于點P.
如圖,⊙O中,半徑CO垂直于直徑AB,D為OC的中點,過D作弦EF∥AB,EB與OC交于點P.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 等腰三角形 | B. | 等邊三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 34和43 | B. | -($\frac{1}{2}$)3和(-$\frac{1}{2}$)3 | C. | -22和 (-2 )2 | D. | |-3|和-|-3| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com